Profiling with onnxruntime#

Links: notebook, html, PDF, python, slides, GitHub

The notebook profiles the execution of an ONNX graph built from a KMeans model and executed with onnxruntime. It then study the decomposition of one einsum equation into more simple operators.

from jyquickhelper import add_notebook_menu
add_notebook_menu()

%matplotlib inline

%load_ext mlprodict

KMeans#

Builds a KMeans#

from sklearn.datasets import make_classification
X, y = make_classification(100000)

from sklearn.cluster import KMeans
km = KMeans(max_iter=10)
km.fit(X)

KMeans(max_iter=10)

import numpy
from mlprodict.onnx_conv import to_onnx
onx = to_onnx(km, X[:1].astype(numpy.float32))

%onnxview onx

Json#

Another way to look into a model.

from mlprodict.onnxrt import OnnxInference

oinf = OnnxInference(onx)
js = oinf.to_json()

import json
from io import StringIO
from jyquickhelper import JSONJS
JSONJS(json.load(StringIO(oinf.to_json())))

Profiling#

from mlprodict.onnxrt import OnnxInference

oinf = OnnxInference(onx, runtime="onnxruntime1",
                     runtime_options={"enable_profiling": True})

for i in range(0, 111):
    oinf.run({"X": X.astype(numpy.float32)})

df = oinf.get_profiling(as_df=True)
df
cat pid tid dur ts ph name args_op_name args_provider args_graph_index args_parameter_size args_thread_scheduling_stats args_exec_plan_index args_activation_size args_output_size
0 Session 106368 299276 596 12 X model_loading_array NaN NaN NaN NaN NaN NaN NaN NaN
1 Session 106368 299276 6925 670 X session_initialization NaN NaN NaN NaN NaN NaN NaN NaN
2 Node 106368 299276 1 34854 X Re_ReduceSumSquare_fence_before ReduceSumSquare NaN NaN NaN NaN NaN NaN NaN
3 Node 106368 299276 2939 34869 X Re_ReduceSumSquare_kernel_time ReduceSumSquare CPUExecutionProvider 0 0 {'main_thread': {'thread_pool_name': 'session-... 0 8000000 400000
4 Node 106368 299276 0 37872 X Re_ReduceSumSquare_fence_after ReduceSumSquare NaN NaN NaN NaN NaN NaN NaN
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2550 Node 106368 299276 0 2394227 X Ar_ArgMin_fence_before ArgMin NaN NaN NaN NaN NaN NaN NaN
2551 Node 106368 299276 3511 2394228 X Ar_ArgMin_kernel_time ArgMin CPUExecutionProvider 5 0 {'main_thread': {'thread_pool_name': 'session-... 5 3200000 800000
2552 Node 106368 299276 0 2397761 X Ar_ArgMin_fence_after ArgMin NaN NaN NaN NaN NaN NaN NaN
2553 Session 106368 299276 11774 2385990 X SequentialExecutor::Execute NaN NaN NaN NaN NaN NaN NaN NaN
2554 Session 106368 299276 11789 2385982 X model_run NaN NaN NaN NaN NaN NaN NaN NaN

2555 rows × 15 columns

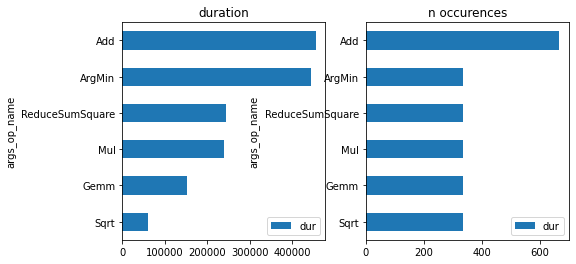
import matplotlib.pyplot as plt
gr_dur = df[['dur', "args_op_name"]].groupby("args_op_name").sum().sort_values('dur')
gr_n = df[['dur', "args_op_name"]].groupby("args_op_name").count().sort_values('dur')
gr_n = gr_n.loc[gr_dur.index, :]

fig, ax = plt.subplots(1, 2, figsize=(8, 4))
gr_dur.plot.barh(ax=ax[0])
gr_n.plot.barh(ax=ax[1])
ax[0].set_title("duration")
ax[1].set_title("n occurences");
../_images/onnx_profile_ort_17_0.png 
gr2 = df.loc[(df.args_op_name == 'Add') & (df.dur > 10), ['dur', "name"]].groupby("name").sum().sort_values('dur')
gr2.plot.barh(figsize=(10, 4));
../_images/onnx_profile_ort_18_0.png

onnxruntime#

from onnxruntime import InferenceSession, RunOptions, SessionOptions
so = SessionOptions()
so.enable_profiling = True
sess = InferenceSession(onx.SerializeToString(), so)

for i in range(0, 111):
    sess.run(None, {'X': X.astype(numpy.float32)}, )

prof = sess.end_profiling()
prof

'onnxruntime_profile__2021-05-13_13-58-59.json'

with open(prof, "r") as f:
    js = json.load(f)

js[:3]

[{'cat': 'Session',
  'pid': 106368,
  'tid': 299276,
  'dur': 450,
  'ts': 6,
  'ph': 'X',
  'name': 'model_loading_array',
  'args': {}},
 {'cat': 'Session',
  'pid': 106368,
  'tid': 299276,
  'dur': 3068,
  'ts': 498,
  'ph': 'X',
  'name': 'session_initialization',
  'args': {}},
 {'cat': 'Node',
  'pid': 106368,
  'tid': 299276,
  'dur': 1,
  'ts': 39069,
  'ph': 'X',
  'name': 'Re_ReduceSumSquare_fence_before',
  'args': {'op_name': 'ReduceSumSquare'}}]

from pandas import DataFrame
from mlprodict.onnxrt.ops_whole.session import OnnxWholeSession

df = DataFrame(OnnxWholeSession.process_profiling(js))
df
cat pid tid dur ts ph name args_op_name args_provider args_graph_index args_parameter_size args_thread_scheduling_stats args_exec_plan_index args_activation_size args_output_size
0 Session 106368 299276 450 6 X model_loading_array NaN NaN NaN NaN NaN NaN NaN NaN
1 Session 106368 299276 3068 498 X session_initialization NaN NaN NaN NaN NaN NaN NaN NaN
2 Node 106368 299276 1 39069 X Re_ReduceSumSquare_fence_before ReduceSumSquare NaN NaN NaN NaN NaN NaN NaN
3 Node 106368 299276 2804 39081 X Re_ReduceSumSquare_kernel_time ReduceSumSquare CPUExecutionProvider 0 0 {'main_thread': {'thread_pool_name': 'session-... 0 8000000 400000
4 Node 106368 299276 0 41947 X Re_ReduceSumSquare_fence_after ReduceSumSquare NaN NaN NaN NaN NaN NaN NaN
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2550 Node 106368 299276 0 2530548 X Ar_ArgMin_fence_before ArgMin NaN NaN NaN NaN NaN NaN NaN
2551 Node 106368 299276 3501 2530550 X Ar_ArgMin_kernel_time ArgMin CPUExecutionProvider 5 0 {'main_thread': {'thread_pool_name': 'session-... 5 3200000 800000
2552 Node 106368 299276 0 2534074 X Ar_ArgMin_fence_after ArgMin NaN NaN NaN NaN NaN NaN NaN
2553 Session 106368 299276 14679 2519397 X SequentialExecutor::Execute NaN NaN NaN NaN NaN NaN NaN NaN
2554 Session 106368 299276 14701 2519386 X model_run NaN NaN NaN NaN NaN NaN NaN NaN

2555 rows × 15 columns

Einsum: bsnh,btnh->bnts#

This section looks into the ONNX graph produces by the decomposition of an einsum equation into more simple ONNX operator (no einsum).

Three implementations#

from mlprodict.testing.einsum import einsum as onx_einsum
from mlprodict.testing.einsum.einsum_fct import _einsum, enumerate_cached_einsum
from numpy import einsum as np_einsum

First classic numpy.

equation = "bsnh,btnh->bnts"

N = 2
inputs = [numpy.random.randn(N, N, N, N).astype(numpy.float32),
          numpy.random.randn(N, N, N, N).astype(numpy.float32)]
np_einsum(equation, *inputs)

array([[[[-2.373884  , -0.63942796],
         [ 1.0523143 ,  5.659873  ]],
        [[ 2.589915  , -0.18050319],
         [-0.6200199 ,  3.793615  ]]],

       [[[-0.37409338,  0.19822143],
         [ 1.2049038 ,  3.1882448 ]],
        [[-0.05218329,  0.87404007],
         [ 0.12789296,  1.4745121 ]]]], dtype=float32)

Then einsum executed by onnxruntime:

onx_einsum(equation, *inputs, runtime='onnxruntime1', optimize=True, verbose=1, decompose=False)

0.0026 best='sbhn,sthn->shtb': 100%|██████████| 121/121 [00:01<00:00, 85.29it/s]

array([[[[-2.373884  , -0.63942796],
         [ 1.0523144 ,  5.659873  ]],

        [[ 2.589915  , -0.18050319],
         [-0.62002003,  3.793615  ]]],


       [[[-0.37409338,  0.19822143],
         [ 1.2049038 ,  3.1882448 ]],

        [[-0.05218329,  0.87404007],
         [ 0.12789296,  1.474512  ]]]], dtype=float32)

obj = _einsum(equation, runtime='onnxruntime1', optimize=True, verbose=1,
              decompose=False, dtype=inputs[0].dtype)

%onnxview obj.onnx_

Same equation but decomposed.

obj = _einsum(equation, runtime='onnxruntime1', optimize=True, verbose=1,
              decompose=True, dtype=inputs[0].dtype)

0.0025 best='hsnt,hbnt->hnbs': 100%|██████████| 121/121 [00:03<00:00, 34.54it/s]

%onnxview obj.onnx_

onx_einsum(equation, *inputs, runtime='onnxruntime1', optimize=True, verbose=1)

array([[[[-2.373884  , -0.63942796],
         [ 1.0523144 ,  5.659873  ]],
        [[ 2.589915  , -0.18050319],
         [-0.62002003,  3.793615  ]]],

       [[[-0.37409338,  0.19822143],
         [ 1.2049038 ,  3.1882448 ]],
        [[-0.05218329,  0.87404007],
         [ 0.12789296,  1.474512  ]]]], dtype=float32)

First benchmark#

N = 20
inputs = [numpy.random.randn(N, N, N, N).astype(numpy.float32),
          numpy.random.randn(N, N, N, N).astype(numpy.float32)]

numpy.einsum

%timeit numpy.einsum(equation, *inputs)

4.14 ms ± 350 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

onnxruntime einsum

%timeit onx_einsum(equation, *inputs, runtime='onnxruntime1', optimize=True, verbose=1, decompose=False)

736 µs ± 11.2 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

onnxruntime decomposed einsum

%timeit onx_einsum(equation, *inputs, runtime='onnxruntime1', optimize=True, verbose=1)

525 µs ± 12.4 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

Let’s disable the optimization to see the difference. The optimization goes through all the permutation of the letters of the equation and compares the computation time to find the best one.

%timeit onx_einsum(equation, *inputs, runtime='onnxruntime1', optimize=False, verbose=1, decompose=False)

761 µs ± 46.2 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

It has no significant impact here but it has for the decomposition. The not optimized version is much slower.

%timeit onx_einsum(equation, *inputs, runtime='onnxruntime1', optimize=False, verbose=1)

1.41 ms ± 43.1 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

Profiling of the not optimized version#

Let’s profile the graph obtained with the decomposition.

obj = _einsum(equation, runtime='onnxruntime1', optimize=False, verbose=1,
              decompose=True, dtype=inputs[0].dtype)
onx = obj.onnx_

obj.equation, obj.equation_

('bsnh,btnh->bnts', 'bsnh,btnh->bnts')

from mlprodict.onnxrt import OnnxInference

oinf = OnnxInference(onx, runtime="onnxruntime1",
                     runtime_options={"enable_profiling": True})

d_inputs = {'X0': inputs[0], 'X1': inputs[1]}
for i in range(0, 100):
    oinf.run(d_inputs)

df = oinf.get_profiling(as_df=True)
df.head()
cat pid tid dur ts ph name args_op_name args_provider args_graph_index args_parameter_size args_thread_scheduling_stats args_exec_plan_index args_activation_size args_output_size
0 Session 106368 299276 705 4 X model_loading_array NaN NaN NaN NaN NaN NaN NaN NaN
1 Session 106368 299276 7019 987 X session_initialization NaN NaN NaN NaN NaN NaN NaN NaN
2 Node 106368 299276 1 8320 X Unsqueeze3_2620928306480_fence_before Unsqueeze NaN NaN NaN NaN NaN NaN NaN
3 Node 106368 299276 4 8327 X Unsqueeze3_2620928306480_kernel_time Unsqueeze CPUExecutionProvider 4 8 {'main_thread': {'thread_pool_name': 'session-... 4 640000 640000
4 Node 106368 299276 0 8372 X Unsqueeze3_2620928306480_fence_after Unsqueeze NaN NaN NaN NaN NaN NaN NaN 
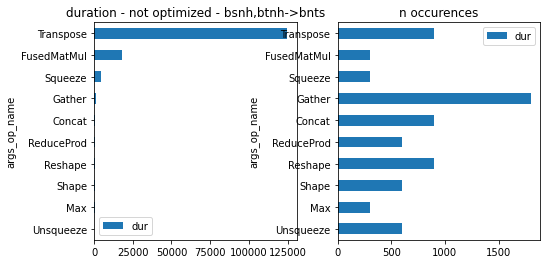
import matplotlib.pyplot as plt
gr_dur = df[['dur', "args_op_name"]].groupby("args_op_name").sum().sort_values('dur')
gr_n = df[['dur', "args_op_name"]].groupby("args_op_name").count().sort_values('dur')
gr_n = gr_n.loc[gr_dur.index, :]

fig, ax = plt.subplots(1, 2, figsize=(8, 4))
gr_dur.plot.barh(ax=ax[0])
gr_n.plot.barh(ax=ax[1])
ax[0].set_title("duration - not optimized - %s" % obj.equation_)
ax[1].set_title("n occurences");
../_images/onnx_profile_ort_54_0.png

Profiling of the optimized version#

obj = _einsum(equation, runtime='onnxruntime1', optimize=True, verbose=1,
              decompose=True, dtype=inputs[0].dtype)
onx = obj.onnx_

obj.equation, obj.equation_

('bsnh,btnh->bnts', 'hsnt,hbnt->hnbs')

The second equation is the optimized equation.

from mlprodict.onnxrt import OnnxInference

oinf = OnnxInference(onx, runtime="onnxruntime1",
                     runtime_options={"enable_profiling": True})

d_inputs = {'X0': inputs[0], 'X1': inputs[1]}
for i in range(0, 100):
    oinf.run(d_inputs)

df = oinf.get_profiling(as_df=True)
df.head()
cat pid tid dur ts ph name args_op_name args_provider args_graph_index args_parameter_size args_thread_scheduling_stats args_exec_plan_index args_activation_size args_output_size
0 Session 106368 299276 1300 6 X model_loading_array NaN NaN NaN NaN NaN NaN NaN NaN
1 Session 106368 299276 7330 1720 X session_initialization NaN NaN NaN NaN NaN NaN NaN NaN
2 Node 106368 299276 1 9376 X Unsqueeze3_2620928202160_fence_before Unsqueeze NaN NaN NaN NaN NaN NaN NaN
3 Node 106368 299276 4 9383 X Unsqueeze3_2620928202160_kernel_time Unsqueeze CPUExecutionProvider 4 8 {'main_thread': {'thread_pool_name': 'session-... 4 640000 640000
4 Node 106368 299276 0 9422 X Unsqueeze3_2620928202160_fence_after Unsqueeze NaN NaN NaN NaN NaN NaN NaN 
gr_dur = df[['dur', "args_op_name"]].groupby("args_op_name").sum().sort_values('dur')
gr_n = df[['dur', "args_op_name"]].groupby("args_op_name").count().sort_values('dur')
gr_n = gr_n.loc[gr_dur.index, :]

fig, ax = plt.subplots(1, 2, figsize=(8, 4))
gr_dur.plot.barh(ax=ax[0])
gr_n.plot.barh(ax=ax[1])
ax[0].set_title("duration - optimized - %s" % obj.equation_)
ax[1].set_title("n occurences");
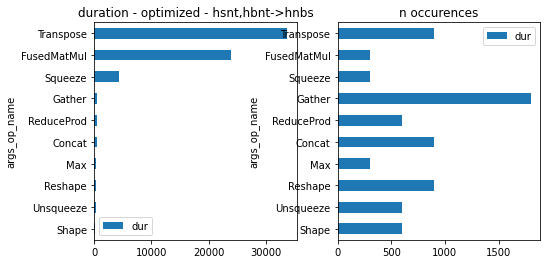
../_images/onnx_profile_ort_60_0.png

onnxruntime was able to fuse MatMul with a transposition. That explains why it is faster.

gr_dur = df[['dur', "args_op_name", "name"]].groupby(["args_op_name", "name"], as_index=False).sum().sort_values('dur')
gr_dur
args_op_name name dur
0 Concat Concat12_fence_after 0
24 Gather Gather1_fence_after 0
25 Gather Gather1_fence_before 0
27 Gather Gather_fence_after 0
60 Transpose Transpose02134_2620928192768_fence_after 0
... ... ... ...
56 Squeeze Squeeze4_2620928194352_kernel_time 4339
59 Transpose Transpose01324_2620928151024_kernel_time 8661
62 Transpose Transpose02134_2620928192768_kernel_time 11487
65 Transpose Transpose13024_2620928192816_kernel_time 13598
11 FusedMatMul MatMul_With_Transpose_kernel_time 23847

72 rows × 3 columns

gr_dur[gr_dur.args_op_name == "Transpose"]
args_op_name name dur
60 Transpose Transpose02134_2620928192768_fence_after 0
57 Transpose Transpose01324_2620928151024_fence_after 0
61 Transpose Transpose02134_2620928192768_fence_before 0
58 Transpose Transpose01324_2620928151024_fence_before 1
64 Transpose Transpose13024_2620928192816_fence_before 1
63 Transpose Transpose13024_2620928192816_fence_after 3
59 Transpose Transpose01324_2620928151024_kernel_time 8661
62 Transpose Transpose02134_2620928192768_kernel_time 11487
65 Transpose Transpose13024_2620928192816_kernel_time 13598

Let’s draw again the graph to see which transpose is is which.

%onnxview onx

The optimized looked into all permutations. We see that the letter ordering should be carefully chosen.

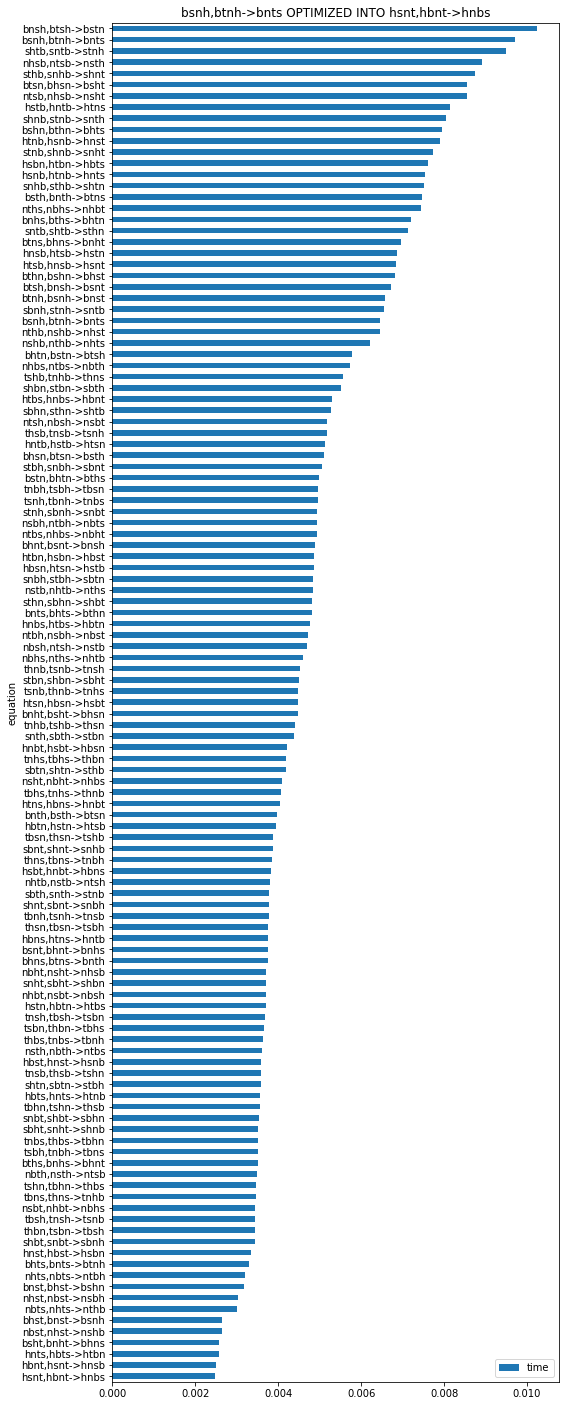
import pandas
df = pandas.DataFrame(obj.timed_permutations_, columns=["time", "equation"])
df = df.sort_values('time')
df = df.set_index("equation")
ax = df.plot.barh(figsize=(8, 25))
ax.set_title("%s OPTIMIZED INTO %s" % (obj.equation, obj.equation_));
../_images/onnx_profile_ort_67_0.png

previous

Precision loss due to float32 conversion with ONNX

next

Time processing for every ONNX nodes in a graph