Einsum decomposition#
Links: notebook, html, PDF, python, slides, GitHub
This notebook shows a way to decompose einsum into a subset of operations (expand_dims, squeeze, transpose, extended matrix multiplication).
from jyquickhelper import add_notebook_menu
add_notebook_menu()
%load_ext mlprodict
Operator explanation with equation bac,cd,def=ebc#
The operator einsum takes an equation and some inputs. Every letter involved in the equation is a loop. Let’s see on one example.
import numpy
m1 = numpy.arange(0, 8).astype(numpy.float32).reshape((2, 2, 2)) + 10
m2 = numpy.arange(0, 4).astype(numpy.float32).reshape((2, 2)) + 100
m3 = numpy.arange(0, 8).astype(numpy.float32).reshape((2, 2, 2)) + 1000
equation = "bac,cd,def->ebc"
truth = numpy.einsum(equation, m1, m2, m3)
truth
array([[[ 8866198., 9864696.],
[12090270., 13152928.]],
[[ 8883886., 9884376.],
[12114390., 13179168.]]], dtype=float32)
This summation is equalent to:
res = numpy.zeros((2, 2, 2))
for a in range(0, 2):
for b in range(0, 2):
for c in range(0, 2):
for d in range(0, 2):
for e in range(0, 2):
for f in range(0, 2):
res[e, b, c] += m1[b, a, c] * m2[c, d] * m3[d, e, f]
res
array([[[ 8866198., 9864696.],
[12090270., 13152928.]],
[[ 8883886., 9884376.],
[12114390., 13179168.]]])
Theoritically, this summation is in this case has a cost of
. However this simple computation is usually much longer
than using matrix multiplications along the path.
is the
cost of the heaviest matrix multiplication in this case). But to do
that, the equation needs to be decomposed into a sequence of matrix
multiplications.
Decomposition of bac,cd,def=ebc#
import numpy
from mlprodict.testing.einsum import (
decompose_einsum_equation, apply_einsum_sequence)
m1 = numpy.arange(0, 8).astype(numpy.float32).reshape((2, 2, 2)) + 10
m2 = numpy.arange(0, 4).astype(numpy.float32).reshape((2, 2)) + 100
m3 = numpy.arange(0, 8).astype(numpy.float32).reshape((2, 2, 2)) + 1000
seq = decompose_einsum_equation("bac,cd,def->ebc")
from jyquickhelper import RenderJsDot
RenderJsDot(seq.to_dot(size=7))
Then the result can be obtained as follows:
apply_einsum_sequence(seq, m1, m2, m3)
array([[[ 8866198., 9864696.],
[12090270., 13152928.]],
[[ 8883886., 9884376.],
[12114390., 13179168.]]], dtype=float32)
operator matmul#
This operator can be used to represent either a multiplication, either a matrix multiplication but it applies only on arrays with the same number of dimensions. It can be broken into multiplication of matrix multiplication.
seq_clean = decompose_einsum_equation("bac,cd,def->ebc", strategy='numpy', clean=True)
RenderJsDot(seq_clean.to_dot(size=7))
Operator transpose_mm is a regular transposition, it takes two inputs but only tranposes the first input before returning it. Operator batch_dot is a matrix multiplication. It is left that way on purpose as it may be implemented with function dot or gemm. The operator distinguishes between 3 kind of axes: batch axes, kept axes, sum(mation) axes. It then reshapes both input matrices with 3D tensors, batch axis, row axis, column axis to use function numpy.dot.
ONNX#
The previous graph can be converted into ONNX.
onx = seq_clean.to_onnx("Y", "X1", "X2", "X3", dtype=numpy.float32)
# with open("einsum.onnx", "wb") as f:
# f.write(onx.SerializeToString())
%onnxview onx
from onnxruntime import InferenceSession
sess = InferenceSession(onx.SerializeToString())
sess.run(None, {'X1': m1.astype(numpy.float32),
'X2': m2.astype(numpy.float32),
'X3': m3.astype(numpy.float32)})[0]
array([[[ 8866198., 9864696.],
[12090270., 13152928.]],
[[ 8883886., 9884376.],
[12114390., 13179168.]]], dtype=float32)
onnxruntime#
import onnx
from onnx import helper, numpy_helper
from onnxruntime import InferenceSession
def make_model1(equation):
model = helper.make_model(
opset_imports=[helper.make_operatorsetid('', 13)],
graph=helper.make_graph(
name='einsum_test',
inputs=[helper.make_tensor_value_info("X", onnx.TensorProto.FLOAT, None),
helper.make_tensor_value_info("Y", onnx.TensorProto.FLOAT, None),
helper.make_tensor_value_info("Z", onnx.TensorProto.FLOAT, None)],
outputs=[helper.make_tensor_value_info("A", onnx.TensorProto.FLOAT, None)],
nodes=[
helper.make_node("Einsum", ["X", "Y", "Z"], ["A"], equation=equation)
]
)
)
return model
model = make_model1("bac,cd,def->ebc")
sess = InferenceSession(model.SerializeToString())
sess.run(None, {'X': m1.astype(numpy.float32),
'Y': m2.astype(numpy.float32),
'Z': m3.astype(numpy.float32)})[0]
array([[[ 8866198., 9864696.],
[12090270., 13152928.]],
[[ 8883886., 9884376.],
[12114390., 13179168.]]], dtype=float32)
Benchmark#
It clearly shows the summation done with the basic algorithm is the slowest.
from mlprodict.onnxrt.validate.validate_helper import measure_time
from tqdm import tqdm
from pandas import DataFrame
def raw_product(m1, m2, m3):
N = m1.shape[0]
res = numpy.zeros((N, N, N))
for a in range(0, N):
for b in range(0, N):
for c in range(0, N):
for d in range(0, N):
for e in range(0, N):
for f in range(0, N):
res[e, b, c] += m1[b, a, c] * m2[c, d] * m3[d, e, f]
return res
def benchmark0(equation):
sess = None
sess2 = None
seq = None
seq2 = None
results = []
for N in tqdm([2, 3, 4, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60]):
m1 = numpy.random.randn(N, N, N)
m2 = numpy.random.randn(N, N)
m3 = numpy.random.randn(N, N, N)
if seq is None:
seq = decompose_einsum_equation(equation, clean=True)
if seq2 is None:
seq2 = decompose_einsum_equation(equation, clean=True, strategy='numpy')
if sess is None:
model = make_model1(equation)
sess = InferenceSession(model.SerializeToString())
if sess2 is None:
onx = seq2.to_onnx("Y", "X1", "X2", "X3", dtype=numpy.float32)
sess2 = InferenceSession(onx.SerializeToString())
res = measure_time(lambda x: numpy.einsum(equation, *x, optimize=True),
[m1, m2, m3],
repeat=10, number=10)
res['name'] = "numpy.einsum"
res["N"] = N
results.append(res)
if N <= 4:
res = measure_time(lambda x: raw_product(*x),
[m1, m2, m3],
repeat=10, number=10)
res['name'] = "raw_product"
res["N"] = N
results.append(res)
res = measure_time(lambda x: apply_einsum_sequence(seq, *x),
[m1, m2, m3],
repeat=10, number=10)
res['name'] = "custom_einsum"
res["N"] = N
results.append(res)
res = measure_time(lambda x: apply_einsum_sequence(seq, *x, matmul_impl="pyf"),
[m1, m2, m3],
repeat=10, number=10)
res['name'] = "dec-matmul"
res["N"] = N
results.append(res)
res = measure_time(lambda x: apply_einsum_sequence(seq2, *x, matmul_impl="pyf"),
[m1, m2, m3],
repeat=10, number=10)
res['name'] = "dec-batch_dot"
res["N"] = N
results.append(res)
res = measure_time(lambda x: sess.run(None, {'X': x[0], 'Y': x[1], 'Z': x[2]}),
[m1.astype(numpy.float32), m2.astype(numpy.float32),
m3.astype(numpy.float32)],
repeat=10, number=10)
res['name'] = "ort-einsum"
res["N"] = N
results.append(res)
res = measure_time(lambda x: sess2.run(None, {'X1': x[0], 'X2': x[1], 'X3': x[2]}),
[m1.astype(numpy.float32), m2.astype(numpy.float32),
m3.astype(numpy.float32)],
repeat=10, number=10)
res['name'] = "ort-matmul"
res["N"] = N
results.append(res)
return DataFrame(results)
df = benchmark0("bac,cd,def->ebc")
df.tail()
C:xavierdupre__home_github_forkscikit-learnsklearnexperimentalenable_hist_gradient_boosting.py:16: UserWarning: Since version 1.0, it is not needed to import enable_hist_gradient_boosting anymore. HistGradientBoostingClassifier and HistGradientBoostingRegressor are now stable and can be normally imported from sklearn.ensemble. warnings.warn( 100%|██████████| 14/14 [00:20<00:00, 1.47s/it]
| average | deviation | min_exec | max_exec | repeat | number | total | name | N | |
|---|---|---|---|---|---|---|---|---|---|
| 82 | 0.065132 | 0.001338 | 0.063801 | 0.068927 | 10 | 10 | 0.651318 | custom_einsum | 60 |
| 83 | 0.051615 | 0.001206 | 0.049987 | 0.053465 | 10 | 10 | 0.516154 | dec-matmul | 60 |
| 84 | 0.062689 | 0.003658 | 0.058949 | 0.073073 | 10 | 10 | 0.626888 | dec-batch_dot | 60 |
| 85 | 0.009917 | 0.000274 | 0.009737 | 0.010686 | 10 | 10 | 0.099166 | ort-einsum | 60 |
| 86 | 0.015518 | 0.001107 | 0.014413 | 0.018179 | 10 | 10 | 0.155178 | ort-matmul | 60 |
import matplotlib.pyplot as plt
piv = df.pivot("N", "name", "average")
piv2 = piv.copy()
np = piv["numpy.einsum"]
for c in piv2.columns:
piv2[c] /= np
fig, ax = plt.subplots(1, 2, figsize=(14, 6))
piv.plot(logy=True, logx=True, ax=ax[0])
ax[0].set_title("Benchmark einsum function\nbac,cd,def->ebc")
piv2.plot(logy=True, logx=True, ax=ax[1])
ax[1].set_title("Benchmark einsum function\n(ratio, baseline=numpy)");
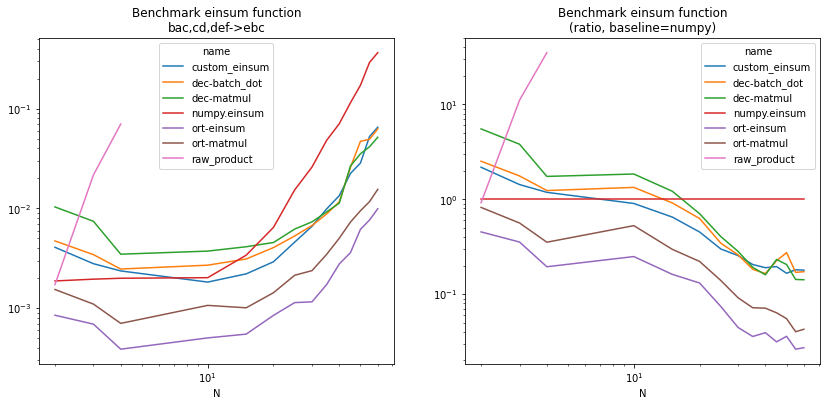
Version dec-matmul is an implementation based on the decomposition
of a simplified einsum into a sequence of transpose, reshape,
(batch_)dot or mul operations. This decomposition is converted into ONNX
and executed with onnxruntime, version ort-matmul. Both versions
are faster than the numpy optimized version.
Another example with bsnh,btnh=bnts#
Another case, more frequent in deep learning.
Decomposition of bsnh,btnh=bnts#
seq2 = decompose_einsum_equation("bsnh,btnh->bnts", strategy='numpy', clean=True)
RenderJsDot(seq2.to_dot(size=7))
ONNX version#
onx2 = seq2.to_onnx("Y", "X1", "X2", dtype=numpy.float32)
%onnxview onx2
Benchmark#
def make_model2(equation):
model = helper.make_model(
opset_imports=[helper.make_operatorsetid('', 13)],
graph=helper.make_graph(
name='einsum_test',
inputs=[helper.make_tensor_value_info("X", onnx.TensorProto.FLOAT, None),
helper.make_tensor_value_info("Y", onnx.TensorProto.FLOAT, None)],
outputs=[helper.make_tensor_value_info("A", onnx.TensorProto.FLOAT, None)],
nodes=[
helper.make_node("Einsum", ["X", "Y"], ["A"], equation=equation)
]
)
)
return model
def benchmark(equation, second_input_size=4):
sess = None
sess2 = None
seq = None
seq2 = None
results = []
for N in tqdm([2, 3, 4, 10, 20, 30, 40]):
m1 = numpy.random.randn(10, N, N, N)
m2 = numpy.random.randn(10 * N ** (second_input_size-1)).reshape((10, ) + (N, ) * (second_input_size-1))
if seq is None:
seq = decompose_einsum_equation(equation, clean=True)
if seq2 is None:
seq2 = decompose_einsum_equation(equation, clean=True, strategy='numpy')
if sess is None:
model = make_model2(equation)
sess = InferenceSession(model.SerializeToString())
if sess2 is None:
onx = seq2.to_onnx("Y", "X1", "X2", dtype=numpy.float32)
sess2 = InferenceSession(onx.SerializeToString())
res = measure_time(lambda x: numpy.einsum(equation, *x, optimize=True),
[m1, m2],
repeat=10, number=10)
res['name'] = "numpy.einsum"
res["N"] = N
results.append(res)
res = measure_time(lambda x: apply_einsum_sequence(seq, *x),
[m1, m2],
repeat=10, number=10)
res['name'] = "custom_einsum"
res["N"] = N
results.append(res)
res = measure_time(lambda x: apply_einsum_sequence(seq, *x, matmul_impl="pyf"),
[m1, m2],
repeat=10, number=10)
res['name'] = "dec-matmul"
res["N"] = N
results.append(res)
res = measure_time(lambda x: apply_einsum_sequence(seq2, *x, matmul_impl="pyf"),
[m1, m2],
repeat=10, number=10)
res['name'] = "dec-batch_dot"
res["N"] = N
results.append(res)
res = measure_time(lambda x: sess.run(None, {'X': x[0], 'Y': x[1]}),
[m1.astype(numpy.float32), m2.astype(numpy.float32),
m3.astype(numpy.float32)],
repeat=10, number=10)
res['name'] = "ort-einsum"
res["N"] = N
results.append(res)
res = measure_time(lambda x: sess2.run(None, {'X1': x[0], 'X2': x[1]}),
[m1.astype(numpy.float32), m2.astype(numpy.float32),
m3.astype(numpy.float32)],
repeat=10, number=10)
res['name'] = "ort-matmul"
res["N"] = N
results.append(res)
return DataFrame(results)
df = benchmark("bsnh,btnh->bnts")
df.tail()
100%|██████████| 7/7 [00:13<00:00, 1.93s/it]
| average | deviation | min_exec | max_exec | repeat | number | total | name | N | |
|---|---|---|---|---|---|---|---|---|---|
| 37 | 0.229418 | 0.020792 | 0.217997 | 0.291032 | 10 | 10 | 2.294175 | custom_einsum | 40 |
| 38 | 0.160575 | 0.005435 | 0.150772 | 0.167411 | 10 | 10 | 1.605746 | dec-matmul | 40 |
| 39 | 0.112844 | 0.011305 | 0.102173 | 0.141890 | 10 | 10 | 1.128436 | dec-batch_dot | 40 |
| 40 | 0.051181 | 0.003533 | 0.047244 | 0.057054 | 10 | 10 | 0.511815 | ort-einsum | 40 |
| 41 | 0.078827 | 0.008735 | 0.067893 | 0.099156 | 10 | 10 | 0.788271 | ort-matmul | 40 |
piv = df.pivot("N", "name", "average")
piv2 = piv.copy()
np = piv["numpy.einsum"]
for c in piv2.columns:
piv2[c] /= np
fig, ax = plt.subplots(1, 2, figsize=(14, 6))
piv.plot(logy=True, logx=True, ax=ax[0])
ax[0].set_title("Benchmark einsum function\nbsnh,btnh->bnts")
piv2.plot(logy=True, logx=True, ax=ax[1])
ax[1].set_title("Benchmark einsum function\n(ratio, baseline=numpy)");
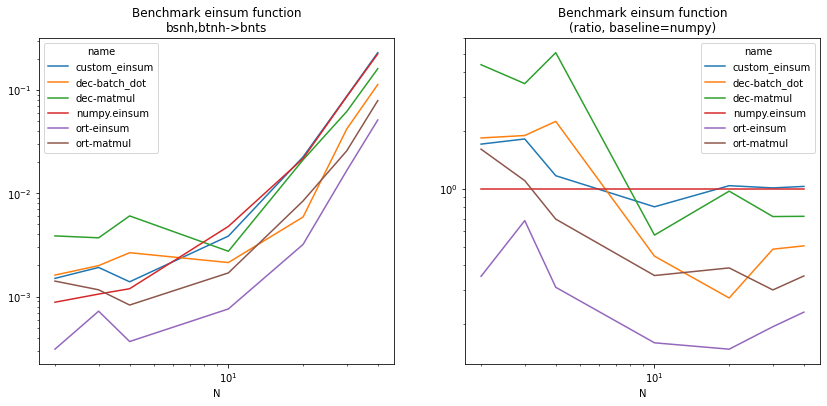
Permutation#
Einsum’s algorithm started by aligning all matrices involved in the computation to the same dimension in the same order. But which order is the best, that’s the question.
equation = "bsnh,btnh->bnts"
letters = list(sorted(set([c for c in equation if "a" <= c < "z"])))
letters
['b', 'h', 'n', 's', 't']
from itertools import permutations
def benchmark_perm(equation, number=5, second_input_size=4, repeat=3, N=15):
def n_operator(seq, name):
n = 0
for op in seq:
if op.name == name:
n += 1
return n
def n_onnx_op(onx, name):
n = 0
for op in onx.graph.node:
if op.op_type == name:
n += 1
return n
def get_kind(seq):
n = 0
for op in seq:
if op.name == 'batch_dot':
return op.get_dot_kind()
return None
m1 = numpy.random.randn(N, N, N, N)
m2 = numpy.random.randn(N ** second_input_size).reshape((N, ) * second_input_size)
results = []
for perm in tqdm(list(permutations(letters))):
replace = {d: c for c, d in zip(letters, perm)}
eq = equation
for k, v in replace.items():
eq = eq.replace(k, v.upper())
eq = eq.lower()
seq = decompose_einsum_equation(eq, clean=True)
seq2 = decompose_einsum_equation(eq, clean=True, strategy='numpy')
model = make_model2(eq)
sess = InferenceSession(model.SerializeToString())
onx = seq2.to_onnx("Y", "X1", "X2", dtype=numpy.float32)
sess2 = InferenceSession(onx.SerializeToString())
n_tra = n_operator(seq2, 'transpose')
n_tra_onnx = n_onnx_op(onx, 'Transpose')
n_gemm_onnx = n_onnx_op(onx, 'Gemm')
kind = get_kind(seq2)
res = measure_time(lambda x: numpy.einsum(eq, *x, optimize=True),
[m1, m2],
repeat=repeat, number=number)
res['name'] = "numpy.einsum"
res["N"] = N
res["eq"] = eq
results.append(res)
res = measure_time(lambda x: apply_einsum_sequence(seq, *x),
[m1, m2],
repeat=repeat, number=number)
res['name'] = "custom_einsum"
res["N"] = N
res["eq"] = eq
res['transpose'] = n_tra
res['kind'] = kind
results.append(res)
res = measure_time(lambda x: apply_einsum_sequence(seq, *x, matmul_impl="pyf"),
[m1, m2],
repeat=repeat, number=number)
res['name'] = "dec-matmul"
res["N"] = N
res["eq"] = eq
res['transpose'] = n_tra
res['kind'] = kind
results.append(res)
res = measure_time(lambda x: apply_einsum_sequence(seq2, *x, matmul_impl="pyf"),
[m1, m2],
repeat=repeat, number=number)
res['name'] = "dec-batch_dot"
res["N"] = N
res["eq"] = eq
res['transpose'] = n_tra
res['kind'] = kind
results.append(res)
res = measure_time(lambda x: sess.run(None, {'X': x[0], 'Y': x[1]}),
[m1.astype(numpy.float32), m2.astype(numpy.float32),
m3.astype(numpy.float32)],
repeat=repeat, number=number)
res['name'] = "ort-einsum"
res["N"] = N
res["eq"] = eq
res['transpose'] = n_tra_onnx
res['gemm'] = n_gemm_onnx
results.append(res)
res = measure_time(lambda x: sess2.run(None, {'X1': x[0], 'X2': x[1]}),
[m1.astype(numpy.float32), m2.astype(numpy.float32),
m3.astype(numpy.float32)],
repeat=repeat, number=number)
res['name'] = "ort-matmul"
res["N"] = N
res["eq"] = eq
res['transpose'] = n_tra_onnx
res['gemm'] = n_gemm_onnx
results.append(res)
return DataFrame(results)
df = benchmark_perm("bsnh,btnh->bnts", number=4)
df.tail()
100%|██████████| 120/120 [00:11<00:00, 10.23it/s]
| average | deviation | min_exec | max_exec | repeat | number | total | name | N | eq | transpose | kind | gemm | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 715 | 0.006162 | 0.000038 | 0.006128 | 0.006216 | 3 | 4 | 0.018485 | custom_einsum | 15 | thns,tbns->tnbh | 3.0 | NN | NaN |
| 716 | 0.002343 | 0.000046 | 0.002294 | 0.002405 | 3 | 4 | 0.007029 | dec-matmul | 15 | thns,tbns->tnbh | 3.0 | NN | NaN |
| 717 | 0.001645 | 0.000035 | 0.001610 | 0.001694 | 3 | 4 | 0.004934 | dec-batch_dot | 15 | thns,tbns->tnbh | 3.0 | NN | NaN |
| 718 | 0.000833 | 0.000015 | 0.000820 | 0.000853 | 3 | 4 | 0.002498 | ort-einsum | 15 | thns,tbns->tnbh | 4.0 | NaN | 0.0 |
| 719 | 0.001251 | 0.000012 | 0.001238 | 0.001268 | 3 | 4 | 0.003753 | ort-matmul | 15 | thns,tbns->tnbh | 4.0 | NaN | 0.0 |
df = df.sort_values("average").reset_index(drop=True)
df.head()
| average | deviation | min_exec | max_exec | repeat | number | total | name | N | eq | transpose | kind | gemm | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.000758 | 0.000015 | 0.000738 | 0.000771 | 3 | 4 | 0.002275 | ort-matmul | 15 | hsnt,hbnt->hnbs | 4.0 | NaN | 0.0 |
| 1 | 0.000770 | 0.000023 | 0.000739 | 0.000793 | 3 | 4 | 0.002310 | ort-matmul | 15 | hnts,hbts->htbn | 4.0 | NaN | 0.0 |
| 2 | 0.000778 | 0.000020 | 0.000758 | 0.000806 | 3 | 4 | 0.002334 | ort-matmul | 15 | bnst,bhst->bshn | 4.0 | NaN | 0.0 |
| 3 | 0.000783 | 0.000021 | 0.000760 | 0.000812 | 3 | 4 | 0.002350 | ort-matmul | 15 | bnht,bsht->bhsn | 4.0 | NaN | 0.0 |
| 4 | 0.000784 | 0.000011 | 0.000774 | 0.000799 | 3 | 4 | 0.002351 | ort-matmul | 15 | hnst,hbst->hsbn | 4.0 | NaN | 0.0 |
df.tail()
| average | deviation | min_exec | max_exec | repeat | number | total | name | N | eq | transpose | kind | gemm | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 715 | 0.011529 | 0.000882 | 0.010456 | 0.012617 | 3 | 4 | 0.034587 | custom_einsum | 15 | sbnt,shnt->snhb | 3.0 | NN | NaN |
| 716 | 0.011548 | 0.000422 | 0.010967 | 0.011953 | 3 | 4 | 0.034644 | custom_einsum | 15 | htsb,hnsb->hsnt | 3.0 | NN | NaN |
| 717 | 0.013971 | 0.001984 | 0.012279 | 0.016754 | 3 | 4 | 0.041912 | custom_einsum | 15 | nbsh,ntsh->nstb | 3.0 | NN | NaN |
| 718 | 0.014765 | 0.001483 | 0.013366 | 0.016818 | 3 | 4 | 0.044295 | numpy.einsum | 15 | bnsh,btsh->bstn | NaN | NaN | NaN |
| 719 | 0.015813 | 0.002921 | 0.012546 | 0.019636 | 3 | 4 | 0.047438 | numpy.einsum | 15 | nbsh,ntsh->nstb | NaN | NaN | NaN |
piv = df.pivot("eq", "name", "average").sort_values("numpy.einsum")
fig, ax = plt.subplots(1, 1, figsize=(14, 6))
piv.plot(logy=True, logx=True, ax=ax)
ax.set_title("Benchmark einsum function - bsnh,btnh->bnts");
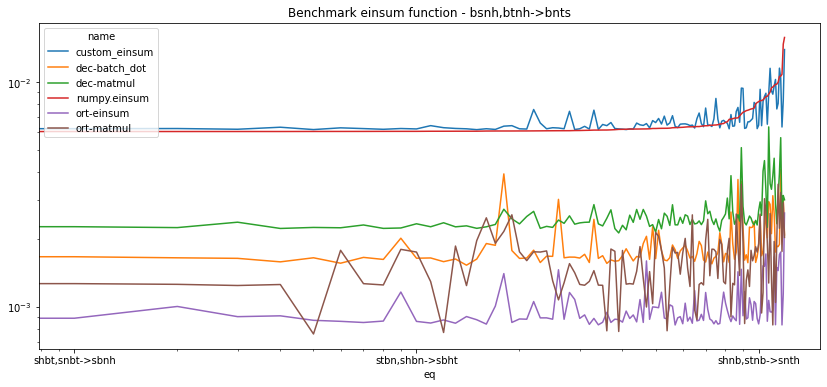
set(df['transpose'].dropna()), set(df['gemm'].dropna()), set(df['kind'].dropna())
({3.0, 4.0}, {0.0}, {'NN'})
Decomposition of bsnh,ctnh=nts#
seq3 = decompose_einsum_equation("bsnh,ctnh->nts", strategy='numpy', clean=True)
RenderJsDot(seq3.to_dot(size=7))
onx3 = seq3.to_onnx("Y", "X1", "X2", dtype=numpy.float32)
%onnxview onx3
Benchmark size#
df = benchmark("bsnh,ctnh->nts")
df.tail()
100%|██████████| 7/7 [00:39<00:00, 5.71s/it]
| average | deviation | min_exec | max_exec | repeat | number | total | name | N | |
|---|---|---|---|---|---|---|---|---|---|
| 37 | 0.043389 | 0.016879 | 0.030195 | 0.077480 | 10 | 10 | 0.433885 | custom_einsum | 40 |
| 38 | 0.015310 | 0.000222 | 0.014909 | 0.015622 | 10 | 10 | 0.153098 | dec-matmul | 40 |
| 39 | 0.013508 | 0.000425 | 0.013148 | 0.014576 | 10 | 10 | 0.135085 | dec-batch_dot | 40 |
| 40 | 0.032725 | 0.000266 | 0.032409 | 0.033212 | 10 | 10 | 0.327254 | ort-einsum | 40 |
| 41 | 0.057384 | 0.002703 | 0.053734 | 0.062845 | 10 | 10 | 0.573841 | ort-matmul | 40 |
piv = df.pivot("N", "name", "average")
piv2 = piv.copy()
np = piv["numpy.einsum"]
for c in piv2.columns:
piv2[c] /= np
fig, ax = plt.subplots(1, 2, figsize=(14, 6))
piv.plot(logy=True, logx=True, ax=ax[0])
ax[0].set_title("Benchmark einsum function\nbsnh,ctnh->nts")
piv2.plot(logy=True, logx=True, ax=ax[1])
ax[1].set_title("Benchmark einsum function\n(ratio, baseline=numpy)");
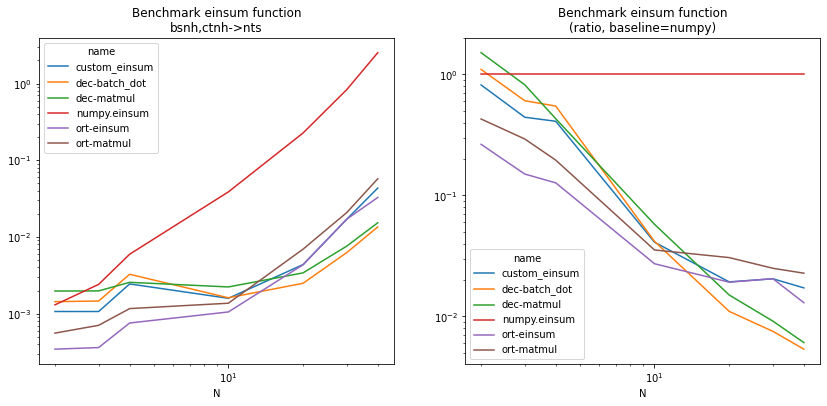
Benchmark permutation#
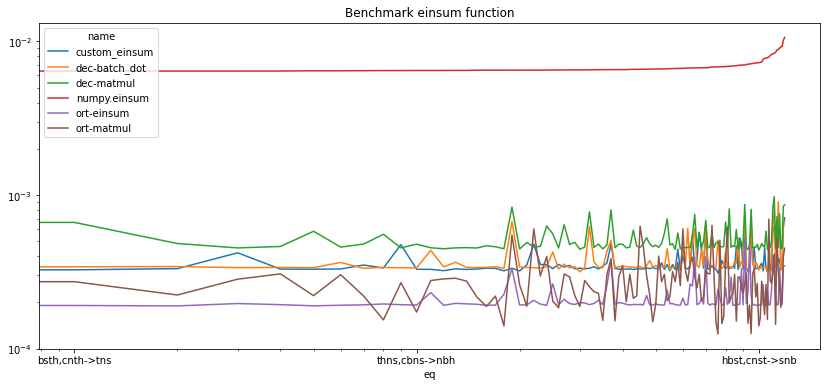
df = benchmark_perm("bsnh,ctnh->nts", number=2, repeat=3, N=10)
100%|██████████| 120/120 [00:06<00:00, 17.41it/s]
df = df.sort_values("average").reset_index(drop=True)
df.head()
| average | deviation | min_exec | max_exec | repeat | number | total | name | N | eq | transpose | kind | gemm | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.000125 | 0.000008 | 0.000118 | 0.000136 | 3 | 2 | 0.000374 | ort-matmul | 10 | bnst,chst->shn | 4.0 | NaN | 0.0 |
| 1 | 0.000126 | 0.000007 | 0.000119 | 0.000136 | 3 | 2 | 0.000377 | ort-matmul | 10 | bhst,cnst->snh | 4.0 | NaN | 0.0 |
| 2 | 0.000141 | 0.000006 | 0.000136 | 0.000150 | 3 | 2 | 0.000422 | ort-matmul | 10 | hbst,cnst->snb | 5.0 | NaN | 0.0 |
| 3 | 0.000141 | 0.000007 | 0.000135 | 0.000151 | 3 | 2 | 0.000423 | ort-matmul | 10 | nbst,chst->shb | 5.0 | NaN | 0.0 |
| 4 | 0.000144 | 0.000007 | 0.000138 | 0.000154 | 3 | 2 | 0.000432 | ort-matmul | 10 | btns,chns->nht | 5.0 | NaN | 0.0 |
set(df['transpose'].dropna()), set(df['gemm'].dropna()), set(df['kind'].dropna())
({3.0, 4.0, 5.0, 6.0}, {0.0}, {'NN'})
piv = df.pivot("eq", "name", "average").sort_values("numpy.einsum")
fig, ax = plt.subplots(1, 1, figsize=(14, 6))
piv.plot(logy=True, logx=True, ax=ax)
ax.set_title("Benchmark einsum function");
Best permutation#
One of the best permutation is bnst,chst->shn.
seq4 = decompose_einsum_equation("bnst,chst->shn", strategy='numpy', clean=True)
RenderJsDot(seq4.to_dot(size=7))
onx4 = seq4.to_onnx("Y", "X1", "X2", dtype=numpy.float32)
%onnxview onx4