Time processing for every ONNX nodes in a graph

Links: notebook, html, PDF, python, slides, GitHub

The following notebook show how long the runtime spends in each node of an ONNX graph.

from jyquickhelper import add_notebook_menu
add_notebook_menu()

%load_ext mlprodict

%matplotlib inline

LogisticRegression

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
clr = LogisticRegression(solver='liblinear')
clr.fit(X_train, y_train)

LogisticRegression(solver='liblinear')

import numpy
from mlprodict.onnx_conv import to_onnx
onx = to_onnx(clr, X_test.astype(numpy.float32))
with open("logreg_time.onnx", "wb") as f:
    f.write(onx.SerializeToString())
# add -l 1 if nothing shows up
%onnxview onx

from mlprodict.onnxrt import OnnxInference
import pandas
oinf = OnnxInference(onx)
res = oinf.run({'X': X_test}, node_time=True)
pandas.DataFrame(list(res[1]))

	i	name	op_type	time
0	0	LinearClassifier	LinearClassifier	0.199603
1	1	Normalizer	Normalizer	0.000091
2	2	Cast	Cast	0.000014
3	3	ZipMap	ZipMap	0.000016

oinf.run({'X': X_test})['output_probability'][:5]

{0: array([8.38235830e-01, 1.21554664e-03, 6.97352537e-04, 7.93823160e-01,
        9.24825077e-01]),
 1: array([0.16162989, 0.39692812, 0.25688601, 0.20607722, 0.07516498]),
 2: array([1.34279470e-04, 6.01856333e-01, 7.42416637e-01, 9.96200831e-05,
        9.94208860e-06])}

Measure time spent in each node

With parameter node_time=True, method run returns the output and time measurement.

exe = oinf.run({'X': X_test}, node_time=True)
exe[1]

[{'i': 0,
  'name': 'LinearClassifier',
  'op_type': 'LinearClassifier',
  'time': 0.00015699999999974068},
 {'i': 1,
  'name': 'Normalizer',
  'op_type': 'Normalizer',
  'time': 5.43000000003957e-05},
 {'i': 2, 'name': 'Cast', 'op_type': 'Cast', 'time': 1.1699999999947863e-05},
 {'i': 3,
  'name': 'ZipMap',
  'op_type': 'ZipMap',
  'time': 1.940000000111297e-05}]

import pandas
pandas.DataFrame(exe[1])

	i	name	op_type	time
0	0	LinearClassifier	LinearClassifier	0.000157
1	1	Normalizer	Normalizer	0.000054
2	2	Cast	Cast	0.000012
3	3	ZipMap	ZipMap	0.000019

Logistic regression: python runtime vs onnxruntime

Function enumerate_validated_operator_opsets implements automated tests for every model with artificial data. Option node_time automatically returns the time spent in each node and does it multiple time.

from mlprodict.onnxrt.validate import enumerate_validated_operator_opsets
res = list(enumerate_validated_operator_opsets(
            verbose=0, models={"LogisticRegression"}, opset_min=12,
            runtime='python', debug=False, node_time=True,
            filter_exp=lambda m, p: p == "b-cl"))

C:xavierdupre__home_github_forkscikit-learnsklearnlinear_model_logistic.py:1356: UserWarning: 'n_jobs' > 1 does not have any effect when 'solver' is set to 'liblinear'. Got 'n_jobs' = 4.
  " = {}.".format(effective_n_jobs(self.n_jobs)))
C:xavierdupre__home_github_forkscikit-learnsklearnlinear_model_logistic.py:1356: UserWarning: 'n_jobs' > 1 does not have any effect when 'solver' is set to 'liblinear'. Got 'n_jobs' = 4.
  " = {}.".format(effective_n_jobs(self.n_jobs)))

import pandas
df = pandas.DataFrame(res[0]['bench-batch'])
df['step'] = df.apply(lambda row: '{}-{}'.format(row['i'], row["name"]), axis=1)
df

	i	name	op_type	time	N	max_time	min_time	repeat	number	step
0	0	LinearClassifier	LinearClassifier	0.000018	1	0.000033	0.000015	20	30	0-LinearClassifier
1	1	Normalizer	Normalizer	0.000017	1	0.000069	0.000012	20	30	1-Normalizer
2	2	Cast	Cast	0.000004	1	0.000009	0.000003	20	30	2-Cast
3	3	ZipMap	ZipMap	0.000005	1	0.000007	0.000004	20	30	3-ZipMap
4	0	LinearClassifier	LinearClassifier	0.000020	10	0.000052	0.000017	20	20	0-LinearClassifier
5	1	Normalizer	Normalizer	0.000015	10	0.000035	0.000013	20	20	1-Normalizer
6	2	Cast	Cast	0.000004	10	0.000013	0.000003	20	20	2-Cast
7	3	ZipMap	ZipMap	0.000004	10	0.000008	0.000004	20	20	3-ZipMap
8	0	LinearClassifier	LinearClassifier	0.000024	100	0.000036	0.000019	10	8	0-LinearClassifier
9	1	Normalizer	Normalizer	0.000018	100	0.000023	0.000015	10	8	1-Normalizer
10	2	Cast	Cast	0.000004	100	0.000006	0.000003	10	8	2-Cast
11	3	ZipMap	ZipMap	0.000007	100	0.000005	0.000004	10	8	3-ZipMap
12	0	LinearClassifier	LinearClassifier	0.000051	1000	0.000057	0.000047	5	5	0-LinearClassifier
13	1	Normalizer	Normalizer	0.000041	1000	0.000045	0.000040	5	5	1-Normalizer
14	2	Cast	Cast	0.000003	1000	0.000004	0.000003	5	5	2-Cast
15	3	ZipMap	ZipMap	0.000004	1000	0.000004	0.000004	5	5	3-ZipMap
16	0	LinearClassifier	LinearClassifier	0.000315	10000	0.000328	0.000315	3	3	0-LinearClassifier
17	1	Normalizer	Normalizer	0.000272	10000	0.000284	0.000256	3	3	1-Normalizer
18	2	Cast	Cast	0.000004	10000	0.000004	0.000004	3	3	2-Cast
19	3	ZipMap	ZipMap	0.000004	10000	0.000004	0.000004	3	3	3-ZipMap
20	0	LinearClassifier	LinearClassifier	0.005634	100000	0.005634	0.005634	1	2	0-LinearClassifier
21	1	Normalizer	Normalizer	0.004671	100000	0.004671	0.004671	1	2	1-Normalizer
22	2	Cast	Cast	0.000024	100000	0.000024	0.000024	1	2	2-Cast
23	3	ZipMap	ZipMap	0.000013	100000	0.000013	0.000013	1	2	3-ZipMap

Following tables shows the time spent in each node, it is relative to the total time. For one observation, the runtime spends 10% of the time in ZipMap, it is only 1% or 2% with 10 observations. These proportions change due to the computing cost of each node.

piv = df.pivot('step', 'N', 'time')
total = piv.sum(axis=0)
piv / total

N	1	10	100	1000	10000	100000
step
0-LinearClassifier	0.410138	0.459103	0.450882	0.512622	0.530490	0.544785
1-Normalizer	0.390060	0.353622	0.350126	0.414227	0.456671	0.451642
2-Cast	0.095729	0.089857	0.074343	0.034398	0.006092	0.002306
3-ZipMap	0.104073	0.097418	0.124649	0.038753	0.006747	0.001267

The python implementation of ZipMap does not change the data but wraps in into a frozen class ArrayZipMapDitionary which mocks a list of dictionaries pandas can ingest to create a DataFrame. The cost is a fixed cost and does not depend on the number of processed rows.

from pyquickhelper.pycode.profiling import profile
bigX = numpy.random.randn(100000, X_test.shape[1]).astype(numpy.float32)
print(profile(lambda: oinf.run({'X': bigX}), pyinst_format="text")[1])

  _     ._   __/__   _ _  _  _ _/_   Recorded: 00:28:08  Samples:  4
 /_//_/// /_/ //_// / //_'/ //     Duration: 0.009     CPU time: 0.031
/   _/                      v3.0.1
Program: c:python372_x64libsite-packagesipykernel_launcher.py -f C:UsersxavieAppDataRoamingjupyterruntimekernel-287476aa-b8ba-4140-902a-b0aad833ffd0.json
0.008 profile  pyquickhelperpycodeprofiling.py:49
`- 0.008 <lambda>  <ipython-input-13-ccd42692a7ed>:3
   `- 0.008 run  mlprodictonnxrtonnx_inference.py:475
      `- 0.008 _run_sequence_runtime  mlprodictonnxrtonnx_inference.py:558
         `- 0.008 run  mlprodictonnxrtonnx_inference_node.py:141
            |- 0.005 run  mlprodictonnxrtops_cpu_op.py:417
            |  `- 0.005 run  mlprodictonnxrtops_cpu_op.py:298
            |     `- 0.005 _run  mlprodictonnxrtops_cpuop_linear_classifier.py:40
            |        |- 0.003 [self]
            |        `- 0.002 argmax  <__array_function__ internals>:2
            |           `- 0.002 argmax  numpycorefromnumeric.py:1112
            |                 [3 frames hidden]  numpy
            |                    0.002 _wrapfunc  numpycorefromnumeric.py:55
            `- 0.003 run  mlprodictonnxrtops_cpu_op.py:383
               `- 0.003 run  mlprodictonnxrtops_cpu_op.py:298
                  `- 0.003 _run  mlprodictonnxrtops_cpuop_normalizer.py:66
                     `- 0.003 norm_l1  mlprodictonnxrtops_cpuop_normalizer.py:42
                        `- 0.003 _norm_L1_inplace  mlprodictonnxrtops_cpuop_normalizer.py:49
                           |- 0.002 [self]
                           `- 0.002 _sum  numpycore_methods.py:36
                                 [2 frames hidden]  numpy

The class ArrayZipMapDictionary is fast to build but has an overhead after that because it builds data when needed.

res = oinf.run({'X': bigX})
prob = res['output_probability']
type(prob)

mlprodict.onnxrt.ops_cpu.op_zipmap.ArrayZipMapDictionary

%timeit pandas.DataFrame(prob)

721 ms ± 54.5 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

list_of_dict = [v.asdict() for v in prob]
%timeit pandas.DataFrame(list_of_dict)

108 ms ± 2.01 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

But if you just need to do the following:

%timeit pandas.DataFrame(prob).values

713 ms ± 56.6 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Then, you can just do that:

print(prob.columns)
%timeit prob.values

[0, 1, 2]
390 ns ± 51.2 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)

And then:

%timeit -n 100 pandas.DataFrame(prob.values, columns=prob.columns)

215 µs ± 82.6 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

We can then compare to what onnxruntime would do when the runtime is called indenpently for each node. We use the runtime named onnxruntime2. Class OnnxInference splits the ONNX graph into multiple ONNX graphs, one for each node, and then calls onnxruntime for each of them indenpently. Python handles the graph logic.

res = list(enumerate_validated_operator_opsets(
            verbose=0, models={"LogisticRegression"}, opset_min=12,
            runtime='onnxruntime2', debug=False, node_time=True))

C:xavierdupre__home_github_forkscikit-learnsklearnlinear_model_logistic.py:1356: UserWarning: 'n_jobs' > 1 does not have any effect when 'solver' is set to 'liblinear'. Got 'n_jobs' = 4.
  " = {}.".format(effective_n_jobs(self.n_jobs)))
C:xavierdupre__home_github_forkscikit-learnsklearnlinear_model_logistic.py:1356: UserWarning: 'n_jobs' > 1 does not have any effect when 'solver' is set to 'liblinear'. Got 'n_jobs' = 4.
  " = {}.".format(effective_n_jobs(self.n_jobs)))
C:xavierdupre__home_github_forkscikit-learnsklearnlinear_model_logistic.py:1356: UserWarning: 'n_jobs' > 1 does not have any effect when 'solver' is set to 'liblinear'. Got 'n_jobs' = 4.
  " = {}.".format(effective_n_jobs(self.n_jobs)))
C:xavierdupre__home_github_forkscikit-learnsklearnlinear_model_logistic.py:1356: UserWarning: 'n_jobs' > 1 does not have any effect when 'solver' is set to 'liblinear'. Got 'n_jobs' = 4.
  " = {}.".format(effective_n_jobs(self.n_jobs)))
C:xavierdupre__home_github_forkscikit-learnsklearnlinear_model_logistic.py:1356: UserWarning: 'n_jobs' > 1 does not have any effect when 'solver' is set to 'liblinear'. Got 'n_jobs' = 4.
  " = {}.".format(effective_n_jobs(self.n_jobs)))
C:xavierdupre__home_github_forkscikit-learnsklearnlinear_model_logistic.py:1356: UserWarning: 'n_jobs' > 1 does not have any effect when 'solver' is set to 'liblinear'. Got 'n_jobs' = 4.
  " = {}.".format(effective_n_jobs(self.n_jobs)))
C:xavierdupre__home_github_forkscikit-learnsklearnlinear_model_logistic.py:1356: UserWarning: 'n_jobs' > 1 does not have any effect when 'solver' is set to 'liblinear'. Got 'n_jobs' = 4.
  " = {}.".format(effective_n_jobs(self.n_jobs)))
C:xavierdupre__home_github_forkscikit-learnsklearnlinear_model_logistic.py:1356: UserWarning: 'n_jobs' > 1 does not have any effect when 'solver' is set to 'liblinear'. Got 'n_jobs' = 4.
  " = {}.".format(effective_n_jobs(self.n_jobs)))
C:xavierdupre__home_github_forkscikit-learnsklearnlinear_model_logistic.py:1356: UserWarning: 'n_jobs' > 1 does not have any effect when 'solver' is set to 'liblinear'. Got 'n_jobs' = 4.
  " = {}.".format(effective_n_jobs(self.n_jobs)))
C:xavierdupre__home_github_forkscikit-learnsklearnlinear_model_logistic.py:1356: UserWarning: 'n_jobs' > 1 does not have any effect when 'solver' is set to 'liblinear'. Got 'n_jobs' = 4.
  " = {}.".format(effective_n_jobs(self.n_jobs)))

res0 = None
for i, r in enumerate(res):
    if "available-ERROR" in r:
        print(i, str(r['available-ERROR']).split("\n")[0])
    elif res0 is None:
        res0 = r

0 Unable to load node 'ZipMap' (output type was inferred)
1 Unable to load node 'ZipMap' (output type was inferred)
4 Unable to load node 'LinearClassifier' (output type was guessed)
5 Unable to load node 'LinearClassifier' (output type was guessed)
6 Unable to load node 'LinearClassifier' (output type was guessed)
7 Unable to load node 'LinearClassifier' (output type was guessed)
8 Unable to load node 'ZipMap' (output type was inferred)
9 Unable to load node 'ZipMap' (output type was inferred)

if '_6ort_run_batch_exc' in res[0]:
    m = "Something went wrong.", res[0]['_6ort_run_batch_exc']
else:
    df = pandas.DataFrame(res0['bench-batch'])
    print(df)
    df['step'] = df.apply(lambda row: '{}-{}'.format(row['i'], row["name"]), axis=1)
    piv = df.pivot('step', 'N', 'time')
    total = piv.sum(axis=0)
    m = piv / total
m

   i              name           op_type      time       N  max_time  0  0  LinearClassifier  LinearClassifier  0.000052       1  0.000190
1  0  LinearClassifier  LinearClassifier  0.000044      10  0.000070
2  0  LinearClassifier  LinearClassifier  0.000071     100  0.000133
3  0  LinearClassifier  LinearClassifier  0.000066    1000  0.000079
4  0  LinearClassifier  LinearClassifier  0.000409   10000  0.000408
5  0  LinearClassifier  LinearClassifier  0.003275  100000  0.003275
   min_time  repeat  number
0  0.000028      20      30
1  0.000031      20      20
2  0.000046      10       8
3  0.000057       5       5
4  0.000365       3       3
5  0.003275       1       2

N	1	10	100	1000	10000	100000
step
0-LinearClassifier	1.0	1.0	1.0	1.0	1.0	1.0

onnxruntime creates a new container each time a ZipMap is executed. That’s whay it takes that much time and the ratio increases when the number of observations increases.

GaussianProcessRegressor

This operator is slow for small batches compare to scikit-learn but closes the gap as the batch size increases. Let’s see where the time goes.

from onnx.defs import onnx_opset_version
from mlprodict.tools.asv_options_helper import get_opset_number_from_onnx
onnx_opset_version(), get_opset_number_from_onnx()

(12, 12)

res = list(enumerate_validated_operator_opsets(
            verbose=1, models={"GaussianProcessRegressor"},
            opset_min=get_opset_number_from_onnx(),
            opset_max=get_opset_number_from_onnx(),
            runtime='python', debug=False, node_time=True,
            filter_exp=lambda m, p: p == "b-reg"))

[enumerate_validated_operator_opsets] opset in [12, 12].

GaussianProcessRegressor    :   0%|          | 0/1 [00:00<?, ?it/s]

[enumerate_compatible_opset] opset in [12, 12].

GaussianProcessRegressor    : 100%|██████████| 1/1 [00:05<00:00,  5.66s/it]

res0 = None
for i, r in enumerate(res):
    if "available-ERROR" in r:
        print(i, str(r['available-ERROR']).split("\n")[0])
    elif res0 is None:
        res0 = r

df = pandas.DataFrame(res0['bench-batch'])
df['step'] = df.apply(lambda row: '{0:02d}-{1}'.format(row['i'], row["name"]), axis=1)
df.head()

	i	name	op_type	time	N	max_time	min_time	repeat	number	step
0	0	kgpd_CDist	CDist	0.000033	1	0.000045	0.000027	20	30	00-kgpd_CDist
1	1	kgpd_Div	Div	0.000009	1	0.000016	0.000007	20	30	01-kgpd_Div
2	2	kgpd_Mul	Mul	0.000006	1	0.000007	0.000005	20	30	02-kgpd_Mul
3	3	kgpd_Sin	Sin	0.000007	1	0.000009	0.000006	20	30	03-kgpd_Sin
4	4	kgpd_Div1	Div	0.000007	1	0.000008	0.000005	20	30	04-kgpd_Div1

pivpy = df.pivot('step', 'N', 'time')
total = pivpy.sum(axis=0)
pivpy / total

N	1	10	100	1000	10000	100000
step
00-kgpd_CDist	0.311496	0.300665	0.244035	0.227984	0.264447	0.288546
01-kgpd_Div	0.082535	0.067193	0.028348	0.011667	0.012230	0.015447
02-kgpd_Mul	0.059840	0.050664	0.018670	0.006959	0.010950	0.012468
03-kgpd_Sin	0.067037	0.086529	0.106165	0.113068	0.102102	0.107563
04-kgpd_Div1	0.061852	0.053088	0.025749	0.010935	0.009810	0.009875
05-kgpd_Pow	0.072520	0.166539	0.361318	0.438253	0.418169	0.404182
06-kgpd_Mul1	0.057508	0.050477	0.020386	0.010334	0.009079	0.010466
07-kgpd_Exp	0.067885	0.098850	0.150876	0.168079	0.165177	0.145106
08-gpr_MatMul	0.137546	0.064570	0.025069	0.009029	0.007134	0.006159
09-gpr_Add	0.081782	0.061424	0.019383	0.003692	0.000903	0.000190

ax = (pivpy / total).T.plot(logx=True, figsize=(14, 4))
ax.set_ylim([0,1])
ax.set_title("Time spent in each node relatively to the total time\npython runtime");

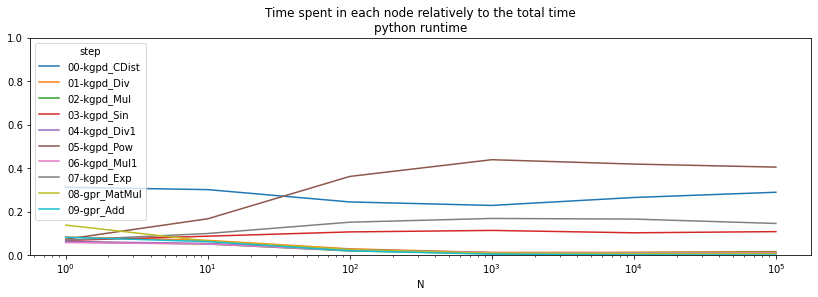
The operator Scan is clearly time consuming when the batch size is small. onnxruntime is more efficient for this one.

res = list(enumerate_validated_operator_opsets(
            verbose=1, models={"GaussianProcessRegressor"},
            opset_min=get_opset_number_from_onnx(),
            opset_max=get_opset_number_from_onnx(),
            runtime='onnxruntime2', debug=False, node_time=True,
            filter_exp=lambda m, p: p == "b-reg"))

[enumerate_validated_operator_opsets] opset in [12, 12].

GaussianProcessRegressor    :   0%|          | 0/1 [00:00<?, ?it/s]

[enumerate_compatible_opset] opset in [12, 12].

GaussianProcessRegressor    : 100%|██████████| 1/1 [00:06<00:00,  6.84s/it]

try:
    df = pandas.DataFrame(res[0]['bench-batch'])
except KeyError as e:
    print("No model available.")
    r, df = None, None
if df is not None:
    df['step'] = df.apply(lambda row: '{0:02d}-{1}'.format(row['i'], row["name"]), axis=1)
    pivort = df.pivot('step', 'N', 'time')
    total = pivort.sum(axis=0)
    r = pivort / total
r

N	1	10	100	1000	10000	100000
step
00-kgpd_CDist	0.114001	0.120884	0.128845	0.148042	0.156776	0.180377
01-kgpd_Div	0.101792	0.098622	0.085983	0.085108	0.086603	0.084520
02-kgpd_Mul	0.099980	0.097547	0.084001	0.064706	0.072849	0.081023
03-kgpd_Sin	0.089632	0.103505	0.194194	0.301002	0.245769	0.260717
04-kgpd_Div1	0.099119	0.096737	0.088709	0.063237	0.095840	0.091635
05-kgpd_Pow	0.108045	0.098307	0.081161	0.064898	0.079015	0.076962
06-kgpd_Mul1	0.098561	0.098475	0.082770	0.063557	0.087732	0.076762
07-kgpd_Exp	0.090019	0.087015	0.086282	0.088542	0.103798	0.087690
08-gpr_MatMul	0.100426	0.102766	0.106220	0.102751	0.069157	0.059617
09-gpr_Add	0.098425	0.096143	0.061836	0.018155	0.002462	0.000696

if r is not None:
    ax = (pivort / total).T.plot(logx=True, figsize=(14, 4))
    ax.set_ylim([0,1])
    ax.set_title("Time spent in each node relatively to the total time\nonnxtunime");

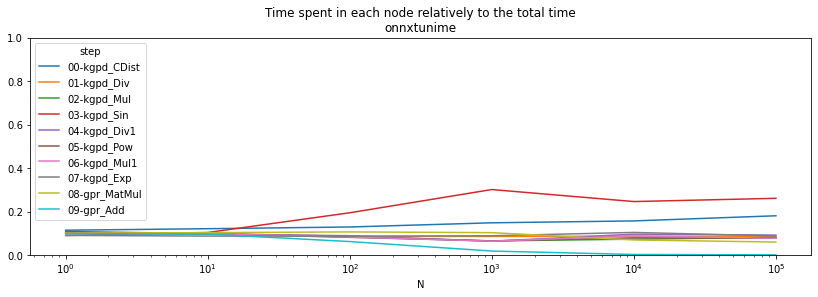
The results are relative. Let’s see which runtime is best node by node.

if r is not None:
    r = (pivort - pivpy) / pivpy
r

N	1	10	100	1000	10000	100000
step
00-kgpd_CDist	-0.239113	-0.367743	-0.630420	-0.703226	-0.677041	-0.631775
01-kgpd_Div	1.564119	1.308106	1.123155	2.333824	2.857590	2.223117
02-kgpd_Mul	2.473648	2.027773	2.149388	3.249448	2.624165	2.828025
03-kgpd_Sin	1.779780	0.881090	0.280401	0.216680	0.311288	0.427768
04-kgpd_Div1	2.331710	1.865534	1.411570	1.642922	4.321977	4.466249
05-kgpd_Pow	2.097502	-0.071724	-0.842765	-0.932321	-0.897065	-0.887837
06-kgpd_Mul1	2.563218	2.067909	1.842112	1.811019	4.263897	3.320524
07-kgpd_Exp	1.756911	0.384288	-0.599693	-0.759241	-0.657668	-0.644029
08-gpr_MatMul	0.517953	1.502798	1.965953	4.201281	4.281286	4.701255
09-gpr_Add	1.502111	1.461452	1.233097	1.247736	0.486358	1.160395

Based on this, onnxruntime is faster for operators Scan, Pow, Exp and slower for all the others.

Measuring the time with a custom dataset

We use the example Comparison of kernel ridge and Gaussian process regression.

import numpy
import pandas
import matplotlib.pyplot as plt
from sklearn.kernel_ridge import KernelRidge
from sklearn.model_selection import GridSearchCV
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import WhiteKernel, ExpSineSquared

rng = numpy.random.RandomState(0)

# Generate sample data
X = 15 * rng.rand(100, 1)
y = numpy.sin(X).ravel()
y += 3 * (0.5 - rng.rand(X.shape[0]))  # add noise

gp_kernel = ExpSineSquared(1.0, 5.0, periodicity_bounds=(1e-2, 1e1))
gpr = GaussianProcessRegressor(kernel=gp_kernel)
gpr.fit(X, y)

C:xavierdupre__home_github_forkscikit-learnsklearngaussian_processkernels.py:409: ConvergenceWarning: The optimal value found for dimension 0 of parameter length_scale is close to the specified lower bound 1e-05. Decreasing the bound and calling fit again may find a better value.
  ConvergenceWarning)
C:xavierdupre__home_github_forkscikit-learnsklearngaussian_processkernels.py:418: ConvergenceWarning: The optimal value found for dimension 0 of parameter periodicity is close to the specified upper bound 10.0. Increasing the bound and calling fit again may find a better value.
  ConvergenceWarning)

GaussianProcessRegressor(kernel=ExpSineSquared(length_scale=1, periodicity=5))

onx = to_onnx(gpr, X_test.astype(numpy.float64))
with open("gpr_time.onnx", "wb") as f:
    f.write(onx.SerializeToString())
%onnxview onx -r 1

from mlprodict.tools import get_ir_version_from_onnx
onx.ir_version = get_ir_version_from_onnx()

oinfpy = OnnxInference(onx, runtime="python")
oinfort = OnnxInference(onx, runtime="onnxruntime2")

runtime==onnxruntime2 tells the class OnnxInference to use onnxruntime for every node independently, there are as many calls as there are nodes in the graph.

respy = oinfpy.run({'X': X_test}, node_time=True)
try:
    resort = oinfort.run({'X': X_test}, node_time=True)
except Exception as e:
    print(e)
    resort = None

if resort is not None:
    df = pandas.DataFrame(respy[1]).merge(pandas.DataFrame(resort[1]), on=["i", "name", "op_type"],
                                        suffixes=("_py", "_ort"))
    df['delta'] = df.time_ort - df.time_py
else:
    df = None
df

	i	name	op_type	time_py	time_ort	delta
0	0	Sc_Scan	Scan	0.007998	0.005970	-0.002028
1	1	kgpd_Transpose	Transpose	0.000032	0.000599	0.000567
2	2	kgpd_Sqrt	Sqrt	0.000063	0.000112	0.000049
3	3	kgpd_Div	Div	0.000143	0.000097	-0.000045
4	4	kgpd_Mul	Mul	0.000038	0.000321	0.000283
5	5	kgpd_Sin	Sin	0.000095	0.000146	0.000051
6	6	kgpd_Div1	Div	0.000027	0.000096	0.000069
7	7	kgpd_Pow	Pow	0.000299	0.000104	-0.000196
8	8	kgpd_Mul1	Mul	0.000032	0.000097	0.000065
9	9	kgpd_Exp	Exp	0.000383	0.000111	-0.000271
10	10	gpr_MatMul	MatMul	0.000080	0.004359	0.004279
11	11	gpr_Add	Add	0.000034	0.000165	0.000131

The following function runs multiple the same inference and aggregates the results node by node.

from mlprodict.onnxrt.validate.validate import benchmark_fct
res = benchmark_fct(lambda X: oinfpy.run({'X': X_test}, node_time=True),
                    X_test, node_time=True)

df = pandas.DataFrame(res)
df[df.N == 100]

	i	name	op_type	time	N	max_time	min_time	repeat	number
24	0	Sc_Scan	Scan	0.004154	100	0.004330	0.003843	10	8
25	1	kgpd_Transpose	Transpose	0.000013	100	0.000019	0.000010	10	8
26	2	kgpd_Sqrt	Sqrt	0.000018	100	0.000022	0.000015	10	8
27	3	kgpd_Div	Div	0.000025	100	0.000092	0.000015	10	8
28	4	kgpd_Mul	Mul	0.000012	100	0.000019	0.000009	10	8
29	5	kgpd_Sin	Sin	0.000057	100	0.000070	0.000050	10	8
30	6	kgpd_Div1	Div	0.000014	100	0.000017	0.000011	10	8
31	7	kgpd_Pow	Pow	0.000172	100	0.000198	0.000155	10	8
32	8	kgpd_Mul1	Mul	0.000020	100	0.000101	0.000009	10	8
33	9	kgpd_Exp	Exp	0.000213	100	0.000249	0.000193	10	8
34	10	gpr_MatMul	MatMul	0.000034	100	0.000047	0.000026	10	8
35	11	gpr_Add	Add	0.000013	100	0.000019	0.000011	10	8

df100 = df[df.N == 100]

%matplotlib inline

fig, ax = plt.subplots(1, 1, figsize=(14, 4))
ax.bar(df100.i, df100.time, align='center', color='orange')
ax.set_xticks(df100.i)
ax.set_yscale('log')
ax.set_xticklabels(df100.op_type)
ax.errorbar(df100.i, df100.time,
            numpy.abs(df100[["min_time", "max_time"]].T.values - df100.time.values.ravel()),
            uplims=True, lolims=True, color='blue')
ax.set_title("Time spent in each node for 100 observations\nGaussianProcess");

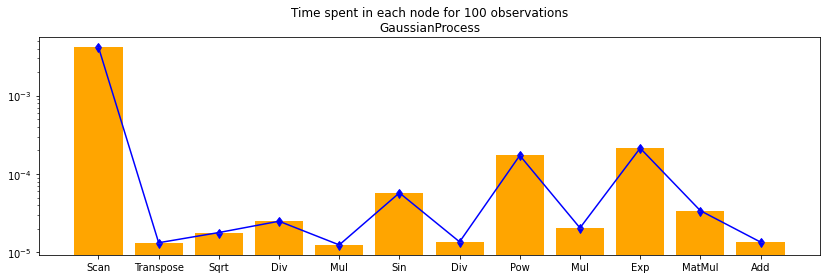
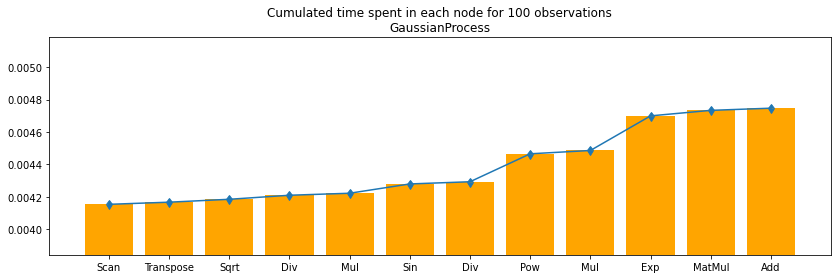
df100c = df100.cumsum()

fig, ax = plt.subplots(1, 1, figsize=(14, 4))
ax.bar(df100.i, df100c.time, align='center', color='orange')
ax.set_xticks(df100.i)
#ax.set_yscale('log')
ax.set_ylim([df100c.min_time.min(), df100c.max_time.max()])
ax.set_xticklabels(df100.op_type)
ax.errorbar(df100.i, df100c.time,
            numpy.abs((df100c[["min_time", "max_time"]].T.values - df100c.time.values.ravel())),
            uplims=True, lolims=True)
ax.set_title("Cumulated time spent in each node for 100 observations\nGaussianProcess");

onnxruntime2 / onnxruntime1

The runtime onnxruntime1 uses onnxruntime for the whole ONNX graph. There is no way to get the computation time for each node except if we create a ONNX graph for each intermediate node.

oinfort1 = OnnxInference(onx, runtime='onnxruntime1')

split = oinfort1.build_intermediate()
split

OrderedDict([('scan0', OnnxInference(...)),
             ('scan1', OnnxInference(...)),
             ('kgpd_transposed0', OnnxInference(...)),
             ('kgpd_Y0', OnnxInference(...)),
             ('kgpd_C03', OnnxInference(...)),
             ('kgpd_C02', OnnxInference(...)),
             ('kgpd_output02', OnnxInference(...)),
             ('kgpd_C01', OnnxInference(...)),
             ('kgpd_Z0', OnnxInference(...)),
             ('kgpd_C0', OnnxInference(...)),
             ('kgpd_output01', OnnxInference(...)),
             ('gpr_Y0', OnnxInference(...)),
             ('GPmean', OnnxInference(...))])

dfs = []
for k, v in split.items():
    print("node", k)
    res = benchmark_fct(lambda x: v.run({'X': x}), X_test)
    df = pandas.DataFrame(res)
    df['name'] = k
    dfs.append(df.reset_index(drop=False))

node scan0
node scan1
node kgpd_transposed0
node kgpd_Y0
node kgpd_C03
node kgpd_C02
node kgpd_output02
node kgpd_C01
node kgpd_Z0
node kgpd_C0
node kgpd_output01
node gpr_Y0
node GPmean

df = pandas.concat(dfs)
df.head()

	index	1	10	100	1000	10000	100000	name
0	average	0.000623	0.000592	0.000754	0.002202	0.017529	0.201192	scan0
1	deviation	0.000115	0.000030	0.000034	0.000026	0.000976	0.000000	scan0
2	min_exec	0.000541	0.000537	0.000657	0.002169	0.016677	0.201192	scan0
3	max_exec	0.000980	0.000639	0.000780	0.002239	0.018896	0.201192	scan0
4	repeat	20.000000	20.000000	10.000000	5.000000	3.000000	1.000000	scan0

df100c = df[df['index'] == "average"]
df100c_min = df[df['index'] == "min_exec"]
df100c_max = df[df['index'] == "max_exec"]
ave = df100c.iloc[:, 4]
ave_min = df100c_min.iloc[:, 4]
ave_max = df100c_max.iloc[:, 4]
ave.shape, ave_min.shape, ave_max.shape
index = numpy.arange(ave.shape[0])

fig, ax = plt.subplots(1, 1, figsize=(14, 4))
ax.bar(index, ave, align='center', color='orange')
ax.set_xticks(index)
ax.set_xticklabels(df100c.name)
for tick in ax.get_xticklabels():
    tick.set_rotation(20)
ax.errorbar(index, ave,
            numpy.abs((numpy.vstack([ave_min.values, ave_max.values]) - ave.values.ravel())),
            uplims=True, lolims=True)
ax.set_title("Cumulated time spent in each node for 100 "
             "observations\nGaussianProcess and onnxruntime1");

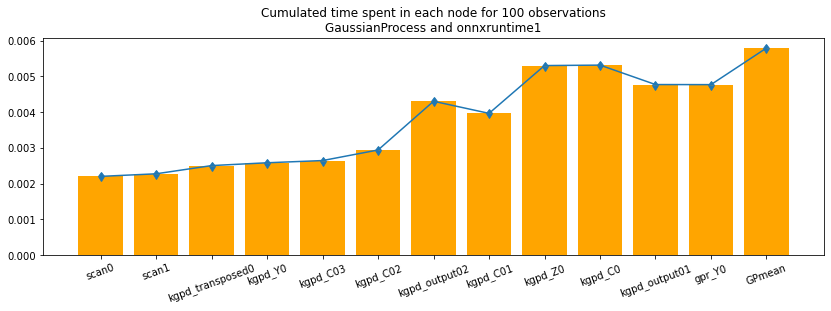
The visual graph helps matching the output names with the operator type. The curve is not monotononic because each experiment computes every output from the start. The number of repetitions should be increased. Documentation of function benchmark_fct tells how to do it.

previous

Profiling with onnxruntime

next

Transfer Learning with ONNX