ONNX graph, single or double floats#

Links: notebook, html, PDF, python, slides, GitHub

The notebook shows discrepencies obtained by using double floats instead of single float in two cases. The second one involves GaussianProcessRegressor.

from jyquickhelper import add_notebook_menu
add_notebook_menu()

Simple case of a linear regression#

A linear regression is simply a matrix multiplication followed by an addition: Y=AX+B. Let’s train one with scikit-learn.

from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
data = load_boston()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
clr = LinearRegression()
clr.fit(X_train, y_train)

LinearRegression()

clr.score(X_test, y_test)

0.7305965839248935

clr.coef_

array([-1.15896254e-01,  3.85174778e-02,  1.59315996e-02,  3.22074735e+00,
       -1.85418374e+01,  3.21813935e+00,  1.12610939e-02, -1.32043742e+00,
        3.67002299e-01, -1.41101521e-02, -1.10152072e+00,  6.17018918e-03,
       -5.71549389e-01])

clr.intercept_

43.97633987084284

Let’s predict with scikit-learn and python.

ypred = clr.predict(X_test)
ypred[:5]

array([17.72795971, 18.69312745, 21.13760633, 16.65607505, 22.47115623])

py_pred = X_test @ clr.coef_ + clr.intercept_
py_pred[:5]

array([17.72795971, 18.69312745, 21.13760633, 16.65607505, 22.47115623])

clr.coef_.dtype, clr.intercept_.dtype

(dtype('float64'), dtype('float64'))

With ONNX#

With ONNX, we would write this operation as follows… We still need to convert everything into single floats = float32.

%load_ext mlprodict

from skl2onnx.algebra.onnx_ops import OnnxMatMul, OnnxAdd
import numpy

onnx_fct = OnnxAdd(OnnxMatMul('X', clr.coef_.astype(numpy.float32), op_version=12),
                   numpy.array([clr.intercept_], dtype=numpy.float32),
                   output_names=['Y'], op_version=12)
onnx_model32 = onnx_fct.to_onnx({'X': X_test.astype(numpy.float32)})

# add -l 1 if nothing shows up
%onnxview onnx_model32

The next line uses a python runtime to compute the prediction.

from mlprodict.onnxrt import OnnxInference
oinf = OnnxInference(onnx_model32, inplace=False)
ort_pred = oinf.run({'X': X_test.astype(numpy.float32)})['Y']
ort_pred[:5]

array([17.727959, 18.693125, 21.137608, 16.656076, 22.471157],
      dtype=float32)

And here is the same with onnxruntime…

from mlprodict.tools.asv_options_helper import get_ir_version_from_onnx
# line needed when onnx is more recent than onnxruntime
onnx_model32.ir_version = get_ir_version_from_onnx()
oinf = OnnxInference(onnx_model32, runtime="onnxruntime1")
ort_pred = oinf.run({'X': X_test.astype(numpy.float32)})['Y']
ort_pred[:5]

array([17.727959, 18.693125, 21.137608, 16.656076, 22.471157],
      dtype=float32)

With double instead of single float#

ONNX was originally designed for deep learning which usually uses floats but it does not mean cannot be used. Every number is converted into double floats.

onnx_fct = OnnxAdd(OnnxMatMul('X', clr.coef_.astype(numpy.float64), op_version=12),
                   numpy.array([clr.intercept_], dtype=numpy.float64),
                   output_names=['Y'], op_version=12)
onnx_model64 = onnx_fct.to_onnx({'X': X_test.astype(numpy.float64)})

And now the python runtime…

oinf = OnnxInference(onnx_model64)
ort_pred = oinf.run({'X': X_test})['Y']
ort_pred[:5]

array([17.72795971, 18.69312745, 21.13760633, 16.65607505, 22.47115623])

And the onnxruntime version of it.

oinf = OnnxInference(onnx_model64, runtime="onnxruntime1")
ort_pred = oinf.run({'X': X_test.astype(numpy.float64)})['Y']
ort_pred[:5]

array([17.72795971, 18.69312745, 21.13760633, 16.65607505, 22.47115623])

And now the GaussianProcessRegressor#

This shows a case

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import DotProduct
gau = GaussianProcessRegressor(alpha=10, kernel=DotProduct())
gau.fit(X_train, y_train)

GaussianProcessRegressor(alpha=10, kernel=DotProduct(sigma_0=1))

from mlprodict.onnx_conv import to_onnx
onnxgau32 = to_onnx(gau, X_train.astype(numpy.float32))
oinf32 = OnnxInference(onnxgau32, runtime="python", inplace=False)
ort_pred32 = oinf32.run({'X': X_test.astype(numpy.float32)})['GPmean']
numpy.squeeze(ort_pred32)[:25]

array([17.25    , 19.59375 , 21.34375 , 17.625   , 21.953125, 30.      ,
       18.875   , 19.625   ,  9.9375  , 20.5     , -0.53125 , 16.375   ,
       16.8125  , 20.6875  , 27.65625 , 16.375   , 39.0625  , 36.0625  ,
       40.71875 , 21.53125 , 29.875   , 30.34375 , 23.53125 , 15.25    ,
       35.5     ], dtype=float32)

onnxgau64 = to_onnx(gau, X_train.astype(numpy.float64))
oinf64 = OnnxInference(onnxgau64, runtime="python", inplace=False)
ort_pred64 = oinf64.run({'X': X_test.astype(numpy.float64)})['GPmean']
numpy.squeeze(ort_pred64)[:25]

array([17.22940605, 19.07756253, 21.000277  , 17.33514034, 22.37701168,
       30.10867125, 18.72937468, 19.2220674 ,  9.74660609, 20.3440565 ,
       -0.1354653 , 16.47852265, 17.12332707, 21.04137646, 27.21477015,
       16.2668399 , 39.31065954, 35.99032274, 40.53761676, 21.51909954,
       29.49016665, 30.22944875, 23.58969906, 14.56499415, 35.28957228])

The differences between the predictions for single floats and double floats…

numpy.sort(numpy.sort(numpy.squeeze(ort_pred32 - ort_pred64)))[-5:]

array([0.51618747, 0.54317928, 0.61256575, 0.63292898, 0.68500585])

Who’s right or wrong… The differences between the predictions with the original model…

pred = gau.predict(X_test.astype(numpy.float64))

numpy.sort(numpy.sort(numpy.squeeze(ort_pred32 - pred)))[-5:]

array([0.51618747, 0.54317928, 0.61256575, 0.63292898, 0.68500585])

numpy.sort(numpy.sort(numpy.squeeze(ort_pred64 - pred)))[-5:]

array([0., 0., 0., 0., 0.])

Double predictions clearly wins.

# add -l 1 if nothing shows up
%onnxview onnxgau64

Saves…#

Let’s keep track of it.

with open("gpr_dot_product_boston_32.onnx", "wb") as f:
    f.write(onnxgau32.SerializePartialToString())
from IPython.display import FileLink
FileLink('gpr_dot_product_boston_32.onnx')
gpr_dot_product_boston_32.onnx
with open("gpr_dot_product_boston_64.onnx", "wb") as f:
    f.write(onnxgau64.SerializePartialToString())
FileLink('gpr_dot_product_boston_64.onnx')
gpr_dot_product_boston_64.onnx

Side by side#

We may wonder where the discrepencies start. But for that, we need to do a side by side.

from mlprodict.onnxrt.validate.side_by_side import side_by_side_by_values
sbs = side_by_side_by_values([(oinf32, {'X': X_test.astype(numpy.float32)}),
                              (oinf64, {'X': X_test.astype(numpy.float64)})])

from pandas import DataFrame
df = DataFrame(sbs)
# dfd = df.drop(['value[0]', 'value[1]', 'value[2]'], axis=1).copy()
df
metric step v[0] v[1] cmp name value[0] shape[0] value[1] shape[1]
0 nb_results -1 9 9.000000e+00 OK NaN NaN NaN NaN NaN
1 abs-diff 0 0 4.902064e-08 OK X [[0.21977, 0.0, 6.91, 0.0, 0.448, 5.602, 62.0,... (127, 13) [[0.21977, 0.0, 6.91, 0.0, 0.448, 5.602, 62.0,... (127, 13)
2 abs-diff 1 0 2.402577e-02 e<0.1 GPmean [[17.25, 19.59375, 21.34375, 17.625, 21.953125... (1, 127) [[17.229406048412784, 19.077562531849253, 21.0... (1, 127)
3 abs-diff 2 0 5.553783e-08 OK kgpd_MatMulcst [[16.8118, 0.26169, 7.67202, 0.57529, 1.13081,... (13, 379) [[16.8118, 0.26169, 7.67202, 0.57529, 1.13081,... (13, 379)
4 abs-diff 3 0 2.421959e-08 OK kgpd_Addcst [1117.718] (1,) [1117.718044648797] (1,)
5 abs-diff 4 0 5.206948e-08 OK gpr_MatMulcst [-0.040681414, -0.37079695, -0.7959402, 0.4380... (379,) [-0.04068141268069173, -0.37079693473728526, -... (379,)
6 abs-diff 5 0 0.000000e+00 OK gpr_Addcst [[0.0]] (1, 1) [[0.0]] (1, 1)
7 abs-diff 6 0 1.856291e-07 OK kgpd_Y0 [[321007.53, 235496.9, 319374.4, 230849.73, 22... (127, 379) [[321007.55279690475, 235496.9156560601, 31937... (127, 379)
8 abs-diff 7 0 1.856291e-07 OK kgpd_C0 [[321007.53, 235496.9, 319374.4, 230849.73, 22... (127, 379) [[321007.55279690475, 235496.9156560601, 31937... (127, 379)
9 abs-diff 8 0 2.402577e-02 e<0.1 gpr_Y0 [17.25, 19.59375, 21.34375, 17.625, 21.953125,... (127,) [17.229406048412784, 19.077562531849253, 21.00... (127,)

The differences really starts for output 'O0' after the matrix multiplication. This matrix melts different number with very different order of magnitudes and that alone explains the discrepencies with doubles and floats on that particular model.

%matplotlib inline
ax = df[['name', 'v[1]']].iloc[1:].set_index('name').plot(kind='bar', figsize=(14,4), logy=True)
ax.set_title("Relative differences for each output between float32 and "
             "float64\nfor a GaussianProcessRegressor");
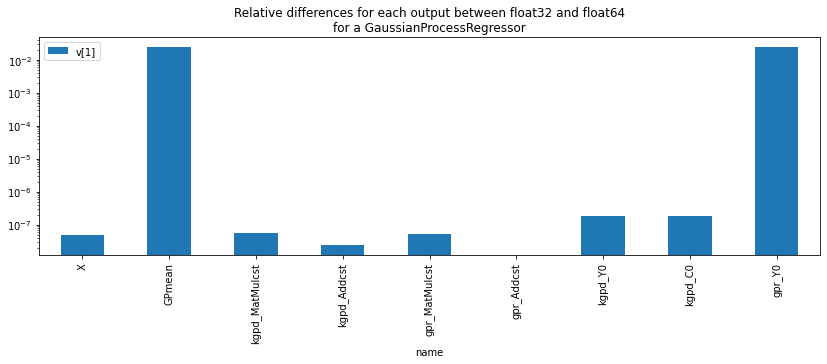
../_images/onnx_float32_and_64_42_0.png

Before going further, let’s check how sensitive the trained model is about converting double into floats.

pg1 = gau.predict(X_test)
pg2 = gau.predict(X_test.astype(numpy.float32).astype(numpy.float64))
numpy.sort(numpy.sort(numpy.squeeze(pg1 - pg2)))[-5:]

array([1.53295696e-06, 1.60621130e-06, 1.65373785e-06, 1.66549580e-06,
       2.36724736e-06])

Having float or double inputs should not matter. We confirm that with the model converted into ONNX.

p1 = oinf64.run({'X': X_test})['GPmean']
p2 = oinf64.run({'X': X_test.astype(numpy.float32).astype(numpy.float64)})['GPmean']
numpy.sort(numpy.sort(numpy.squeeze(p1 - p2)))[-5:]

array([1.53295696e-06, 1.60621130e-06, 1.65373785e-06, 1.66549580e-06,
       2.36724736e-06])

Last verification.

sbs = side_by_side_by_values([(oinf64, {'X': X_test.astype(numpy.float32).astype(numpy.float64)}),
                              (oinf64, {'X': X_test.astype(numpy.float64)})])
df = DataFrame(sbs)
ax = df[['name', 'v[1]']].iloc[1:].set_index('name').plot(kind='bar', figsize=(14,4), logy=True)
ax.set_title("Relative differences for each output between float64 and float64 rounded to float32"
             "\nfor a GaussianProcessRegressor");
../_images/onnx_float32_and_64_48_0.png

previous

ONNX and FFT

next

ONNX side by side