Note
Click here to download the full example code
Benchmark operator LeakyRelu¶
The operator LeakyRelu is equivalent to the function:
. But it could be rewritten into
the following decomposition
. Let’s compare the
two implementation with onnx runtimes.
The ONNX graphs for both implementations of LeakyRely¶
import numpy
from numpy.testing import assert_almost_equal
import matplotlib.pyplot as plt
from pandas import DataFrame
from onnx import TensorProto
from onnxruntime import InferenceSession, get_device
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.algebra.onnx_ops import (
OnnxLeakyRelu, OnnxSign, OnnxMul, OnnxAdd, OnnxDiv,
OnnxGreater, OnnxCast)
from cpyquickhelper.numbers.speed_measure import measure_time
from mlprodict.testing.experimental_c_impl.experimental_c import code_optimisation
from mlprodict.plotting.plotting import onnx_simple_text_plot
from onnxcustom.plotting.plotting_onnx import plot_onnxs
from tqdm import tqdm
print([code_optimisation(), get_device()])
Out:
['AVX-omp=8', 'CPU']
First implementation: the operator LeayRelu.
def build_leaky_relu(alpha=0.5, target_opset=15):
x = OnnxLeakyRelu('X', alpha=alpha, op_version=target_opset,
output_names=['Y'])
return x.to_onnx({'X': FloatTensorType()},
outputs={'Y': FloatTensorType()},
target_opset=target_opset)
onx_leaky = build_leaky_relu()
print(onnx_simple_text_plot(onx_leaky))
Out:
opset: domain='' version=15
input: name='X' type=dtype('float32') shape=()
LeakyRelu(X, alpha=0.50) -> Y
output: name='Y' type=dtype('float32') shape=()
Second option, the formula introduced above must adapted as ONNX operator Sign returns -1 if x is negative and not 0.
def build_leaky_relu_decomposed(alpha=0.5, target_opset=15):
signo = OnnxSign('X', op_version=target_opset)
sign = OnnxDiv(
OnnxAdd(signo, numpy.array([1], dtype=numpy.float32),
op_version=target_opset),
numpy.array([2], dtype=numpy.float32), op_version=target_opset)
fact = OnnxAdd(
OnnxMul(sign, numpy.array([1 - alpha], dtype=numpy.float32),
op_version=target_opset),
numpy.array([alpha], dtype=numpy.float32),
op_version=target_opset)
x = OnnxMul('X', fact, op_version=target_opset,
output_names=['Y'])
return x.to_onnx({'X': FloatTensorType()},
outputs={'Y': FloatTensorType()},
target_opset=target_opset)
onx_leaky_dec = build_leaky_relu_decomposed()
print(onnx_simple_text_plot(onx_leaky_dec))
Out:
opset: domain='' version=15
input: name='X' type=dtype('float32') shape=()
init: name='Ad_Addcst' type=dtype('float32') shape=(1,) -- array([1.], dtype=float32)
init: name='Di_Divcst' type=dtype('float32') shape=(1,) -- array([2.], dtype=float32)
init: name='Mu_Mulcst' type=dtype('float32') shape=(1,) -- array([0.5], dtype=float32)
Identity(Mu_Mulcst) -> Ad_Addcst1
Sign(X) -> Si_output0
Add(Si_output0, Ad_Addcst) -> Ad_C01
Div(Ad_C01, Di_Divcst) -> Di_C0
Mul(Di_C0, Mu_Mulcst) -> Mu_C0
Add(Mu_C0, Ad_Addcst1) -> Ad_C0
Mul(X, Ad_C0) -> Y
output: name='Y' type=dtype('float32') shape=()
Third option, use of operater Greater
def build_leaky_relu_decomposed_greater(alpha=0.5, target_opset=15):
signo = OnnxGreater('X', numpy.array([0], dtype=numpy.float32),
op_version=target_opset)
sign = OnnxCast(signo, to=TensorProto.FLOAT,
op_version=target_opset)
fact = OnnxAdd(
OnnxMul(sign, numpy.array([1 - alpha], dtype=numpy.float32),
op_version=target_opset),
numpy.array([alpha], dtype=numpy.float32),
op_version=target_opset)
x = OnnxMul('X', fact, op_version=target_opset,
output_names=['Y'])
return x.to_onnx({'X': FloatTensorType()},
outputs={'Y': FloatTensorType()},
target_opset=target_opset)
onx_leaky_dec_greater = build_leaky_relu_decomposed_greater()
print(onnx_simple_text_plot(onx_leaky_dec_greater))
Out:
opset: domain='' version=15
input: name='X' type=dtype('float32') shape=()
init: name='Gr_Greatercst' type=dtype('float32') shape=(1,) -- array([0.], dtype=float32)
init: name='Mu_Mulcst' type=dtype('float32') shape=(1,) -- array([0.5], dtype=float32)
Greater(X, Gr_Greatercst) -> Gr_C0
Cast(Gr_C0, to=1) -> Ca_output0
Mul(Ca_output0, Mu_Mulcst) -> Mu_C0
Identity(Mu_Mulcst) -> Ad_Addcst
Add(Mu_C0, Ad_Addcst) -> Ad_C0
Mul(X, Ad_C0) -> Y
output: name='Y' type=dtype('float32') shape=()
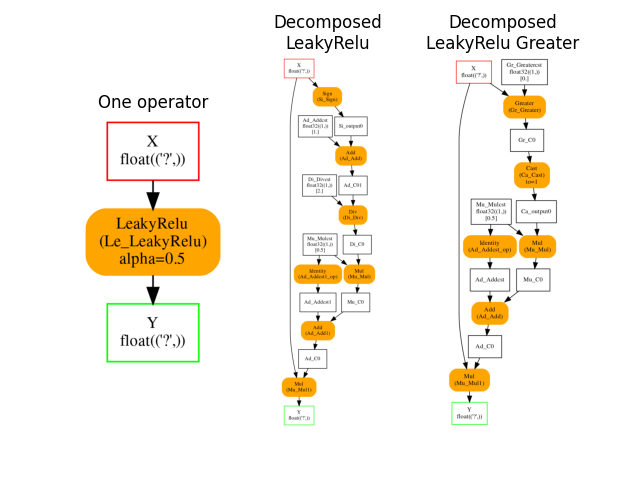
Visually
plot_onnxs(onx_leaky, onx_leaky_dec, onx_leaky_dec_greater,
title=["One operator", "Decomposed\nLeakyRelu",
"Decomposed\nLeakyRelu Greater"])
Out:
array([<AxesSubplot:title={'center':'One operator'}>,
<AxesSubplot:title={'center':'Decomposed\nLeakyRelu'}>,
<AxesSubplot:title={'center':'Decomposed\nLeakyRelu Greater'}>],
dtype=object)
Check that both graph returns are equivalent¶
sess1 = InferenceSession(onx_leaky.SerializeToString(),
providers=['CPUExecutionProvider'])
sess_dec = InferenceSession(onx_leaky_dec.SerializeToString(),
providers=['CPUExecutionProvider'])
sess_dec_greater = InferenceSession(onx_leaky_dec_greater.SerializeToString(),
providers=['CPUExecutionProvider'])
for shape in [(1, ), (10, ), (5, 5), (7, 2, 4)]:
rnd = numpy.random.randn(*shape).astype(numpy.float32)
res1 = sess1.run(None, {'X': rnd})[0]
res_dec = sess_dec.run(None, {'X': rnd})[0]
res_dec_greater = sess_dec_greater.run(None, {'X': rnd})[0]
assert_almost_equal(res1, res_dec)
assert_almost_equal(res1, res_dec_greater)
Benchmark¶
fcts = [('leakyrelu', sess1), ('dec', sess_dec),
('dec_greater', sess_dec_greater)]
N = 100
data = []
for dim in tqdm([10, 128, 256, 512, 1000, 2000]):
for shape in [(N, dim), (dim, N)]:
rnd = numpy.random.randn(*shape).astype(numpy.float32)
for name, sess in fcts:
repeat = int(4001 / dim)
obs = measure_time(
lambda: sess.run(None, {'X': rnd}),
context=dict(rnd=rnd, sess=sess),
div_by_number=True, repeat=repeat, number=200)
obs['name'] = name
obs['N'] = N
obs['dim'] = dim
obs['orient'] = shape[0] == N
obs['shape'] = "%dx%d" % shape
data.append(obs)
df = DataFrame(data)
df[['name', 'N', 'dim', 'average', 'deviation']]
print(df[['name', 'N', 'dim', 'average']])
Out:
0%| | 0/6 [00:00<?, ?it/s]
17%|#6 | 1/6 [00:39<03:15, 39.02s/it]
33%|###3 | 2/6 [00:45<01:20, 20.08s/it]
50%|##### | 3/6 [00:51<00:40, 13.35s/it]
67%|######6 | 4/6 [00:56<00:20, 10.13s/it]
83%|########3 | 5/6 [01:01<00:08, 8.15s/it]
100%|##########| 6/6 [01:05<00:00, 6.81s/it]
100%|##########| 6/6 [01:05<00:00, 10.87s/it]
name N dim average
0 leakyrelu 100 10 0.000067
1 dec 100 10 0.000093
2 dec_greater 100 10 0.000083
3 leakyrelu 100 10 0.000067
4 dec 100 10 0.000093
5 dec_greater 100 10 0.000083
6 leakyrelu 100 128 0.000110
7 dec 100 128 0.000282
8 dec_greater 100 128 0.000166
9 leakyrelu 100 128 0.000108
10 dec 100 128 0.000269
11 dec_greater 100 128 0.000164
12 leakyrelu 100 256 0.000146
13 dec 100 256 0.000478
14 dec_greater 100 256 0.000264
15 leakyrelu 100 256 0.000146
16 dec 100 256 0.000478
17 dec_greater 100 256 0.000263
18 leakyrelu 100 512 0.000241
19 dec 100 512 0.001009
20 dec_greater 100 512 0.000595
21 leakyrelu 100 512 0.000244
22 dec 100 512 0.001016
23 dec_greater 100 512 0.000592
24 leakyrelu 100 1000 0.000469
25 dec 100 1000 0.001377
26 dec_greater 100 1000 0.001011
27 leakyrelu 100 1000 0.000520
28 dec 100 1000 0.001373
29 dec_greater 100 1000 0.001007
30 leakyrelu 100 2000 0.000885
31 dec 100 2000 0.002653
32 dec_greater 100 2000 0.001704
33 leakyrelu 100 2000 0.000893
34 dec 100 2000 0.002570
35 dec_greater 100 2000 0.001678
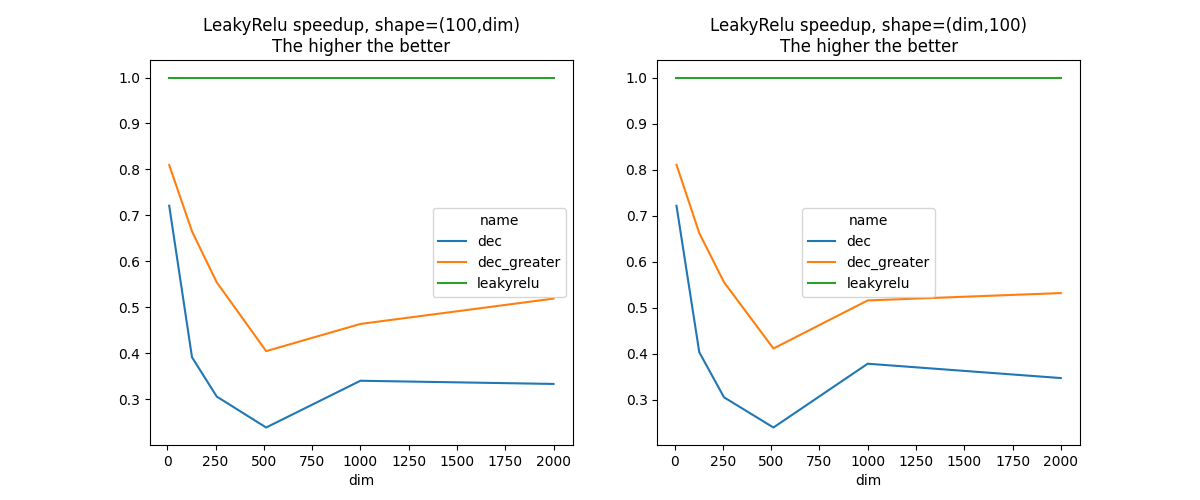
Other to way to look at it.
def speedup(piv):
for c in piv.columns:
if c == 'leakyrelu':
continue
piv[c] = piv['leakyrelu'] / piv[c]
piv['leakyrelu'] = 1
return piv
piv = speedup(df.pivot('shape', 'name', 'average'))
piv
Graph.
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
speedup(df[df.orient].pivot('dim', 'name', 'average')).plot(ax=ax[0])
ax[0].set_title("LeakyRelu speedup, shape=(%d,dim)"
"\nThe higher the better" % N)
speedup(df[~df.orient].pivot('dim', 'name', 'average')).plot(ax=ax[1])
ax[1].set_title("LeakyRelu speedup, shape=(dim,%d)"
"\nThe higher the better" % N)
Out:
Text(0.5, 1.0, 'LeakyRelu speedup, shape=(dim,100)\nThe higher the better')
This kind of benchmark helps finding better implementation of operator runtime.
# plt.show()
Total running time of the script: ( 1 minutes 8.642 seconds)