Note
Click here to download the full example code
Train a scikit-learn neural network with onnxruntime-training on GPU¶
This example leverages example Train a linear regression with onnxruntime-training on GPU in details to train a neural network from scikit-learn on GPU. However, the code is using classes implemented in this module, following the pattern introduced in exemple Train a linear regression with onnxruntime-training.
A neural network with scikit-learn¶
import warnings
from pprint import pprint
import numpy
from pandas import DataFrame
from onnxruntime import get_device, InferenceSession
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import mean_squared_error
from onnxcustom.plotting.plotting_onnx import plot_onnxs
from mlprodict.onnx_conv import to_onnx
from onnxcustom.utils.orttraining_helper import (
add_loss_output, get_train_initializer)
from onnxcustom.training.optimizers import OrtGradientOptimizer
X, y = make_regression(1000, n_features=10, bias=2)
X = X.astype(numpy.float32)
y = y.astype(numpy.float32)
X_train, X_test, y_train, y_test = train_test_split(X, y)
nn = MLPRegressor(hidden_layer_sizes=(10, 10), max_iter=200,
solver='sgd', learning_rate_init=1e-4, alpha=0,
n_iter_no_change=1000, batch_size=10,
momentum=0, nesterovs_momentum=False)
with warnings.catch_warnings():
warnings.simplefilter('ignore')
nn.fit(X_train, y_train)
Score:
print("mean_squared_error=%r" % mean_squared_error(y_test, nn.predict(X_test)))
Out:
mean_squared_error=0.20262958
Conversion to ONNX¶
onx = to_onnx(nn, X_train[:1].astype(numpy.float32), target_opset=15)
plot_onnxs(onx)
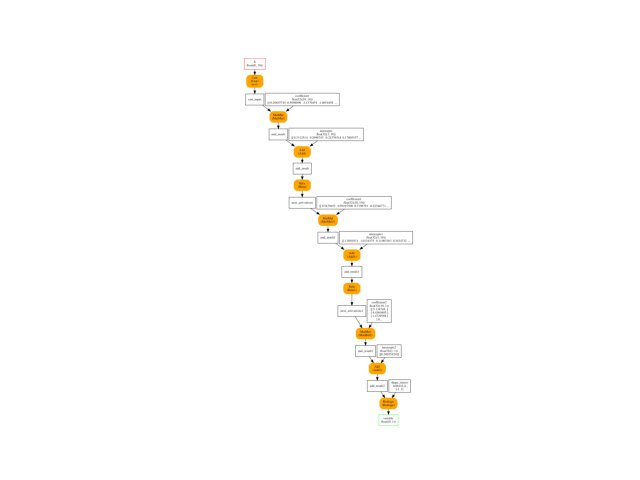
Out:
<AxesSubplot:>
Training graph¶
The loss function is the square function. We use function
add_loss_output.
It does something what is implemented in example
Train a linear regression with onnxruntime-training in details.
onx_train = add_loss_output(onx)
plot_onnxs(onx_train)
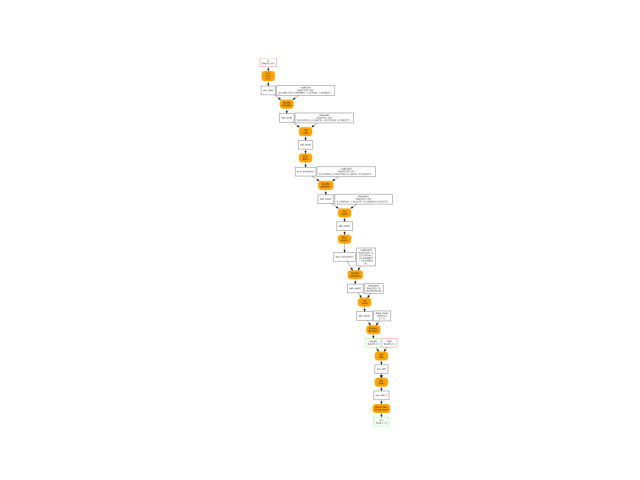
Out:
<AxesSubplot:>
Let’s check inference is working.
sess = InferenceSession(onx_train.SerializeToString(),
providers=['CPUExecutionProvider'])
res = sess.run(None, {'X': X_test, 'label': y_test.reshape((-1, 1))})
print("onnx loss=%r" % (res[0][0, 0] / X_test.shape[0]))
Out:
onnx loss=0.2026282043457031
Let’s retrieve the constant, the weight to optimize. We remove initializer which cannot be optimized.
inits = get_train_initializer(onx)
weights = {k: v for k, v in inits.items() if k != "shape_tensor"}
pprint(list((k, v[0].shape) for k, v in weights.items()))
Out:
[('coefficient', (10, 10)),
('intercepts', (1, 10)),
('coefficient1', (10, 10)),
('intercepts1', (1, 10)),
('coefficient2', (10, 1)),
('intercepts2', (1, 1))]
Training¶
The training session. If GPU is available, it chooses CUDA otherwise it falls back to CPU.
device = "cuda" if get_device().upper() == 'GPU' else 'cpu'
print("device=%r get_device()=%r" % (device, get_device()))
Out:
device='cpu' get_device()='CPU'
The training session.
train_session = OrtGradientOptimizer(
onx_train, list(weights), device=device, verbose=1,
learning_rate=5e-4, warm_start=False, max_iter=200, batch_size=10)
train_session.fit(X, y)
state_tensors = train_session.get_state()
print(train_session.train_losses_)
df = DataFrame({'ort losses': train_session.train_losses_,
'skl losses:': nn.loss_curve_})
df.plot(title="Train loss against iterations", logy=True)
# import matplotlib.pyplot as plt
# plt.show()
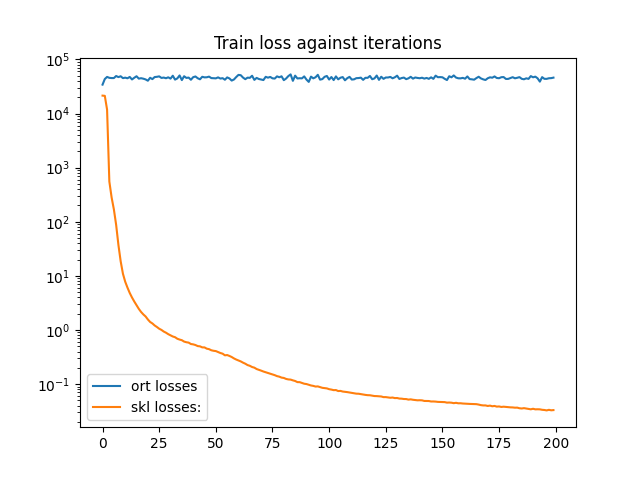
Out:
0%| | 0/200 [00:00<?, ?it/s]
1%|1 | 2/200 [00:00<00:10, 19.76it/s]
2%|2 | 4/200 [00:00<00:09, 19.76it/s]
3%|3 | 6/200 [00:00<00:09, 19.76it/s]
4%|4 | 8/200 [00:00<00:09, 19.78it/s]
5%|5 | 10/200 [00:00<00:09, 19.81it/s]
6%|6 | 12/200 [00:00<00:09, 19.79it/s]
7%|7 | 14/200 [00:00<00:09, 19.81it/s]
8%|8 | 16/200 [00:00<00:09, 19.79it/s]
9%|9 | 18/200 [00:00<00:09, 19.81it/s]
10%|# | 20/200 [00:01<00:09, 19.81it/s]
11%|#1 | 22/200 [00:01<00:08, 19.81it/s]
12%|#2 | 24/200 [00:01<00:08, 19.81it/s]
13%|#3 | 26/200 [00:01<00:08, 19.80it/s]
14%|#4 | 28/200 [00:01<00:08, 19.81it/s]
15%|#5 | 30/200 [00:01<00:08, 19.81it/s]
16%|#6 | 32/200 [00:01<00:08, 19.82it/s]
17%|#7 | 34/200 [00:01<00:08, 19.83it/s]
18%|#8 | 36/200 [00:01<00:08, 19.84it/s]
19%|#9 | 38/200 [00:01<00:08, 19.81it/s]
20%|## | 40/200 [00:02<00:08, 19.83it/s]
21%|##1 | 42/200 [00:02<00:07, 19.85it/s]
22%|##2 | 44/200 [00:02<00:07, 19.84it/s]
23%|##3 | 46/200 [00:02<00:07, 19.84it/s]
24%|##4 | 48/200 [00:02<00:07, 19.84it/s]
25%|##5 | 50/200 [00:02<00:07, 19.83it/s]
26%|##6 | 52/200 [00:02<00:07, 19.83it/s]
27%|##7 | 54/200 [00:02<00:07, 19.78it/s]
28%|##8 | 56/200 [00:02<00:07, 19.79it/s]
29%|##9 | 58/200 [00:02<00:07, 19.83it/s]
30%|### | 60/200 [00:03<00:07, 19.82it/s]
31%|###1 | 62/200 [00:03<00:06, 19.81it/s]
32%|###2 | 64/200 [00:03<00:06, 19.78it/s]
33%|###3 | 66/200 [00:03<00:06, 19.76it/s]
34%|###4 | 68/200 [00:03<00:06, 19.78it/s]
35%|###5 | 70/200 [00:03<00:06, 19.81it/s]
36%|###6 | 72/200 [00:03<00:06, 19.81it/s]
37%|###7 | 74/200 [00:03<00:06, 19.80it/s]
38%|###8 | 76/200 [00:03<00:06, 19.82it/s]
39%|###9 | 78/200 [00:03<00:06, 19.81it/s]
40%|#### | 80/200 [00:04<00:06, 19.82it/s]
41%|####1 | 82/200 [00:04<00:05, 19.83it/s]
42%|####2 | 84/200 [00:04<00:05, 19.82it/s]
43%|####3 | 86/200 [00:04<00:05, 19.82it/s]
44%|####4 | 88/200 [00:04<00:05, 19.82it/s]
45%|####5 | 90/200 [00:04<00:05, 19.84it/s]
46%|####6 | 92/200 [00:04<00:05, 19.83it/s]
47%|####6 | 94/200 [00:04<00:05, 19.83it/s]
48%|####8 | 96/200 [00:04<00:05, 19.80it/s]
49%|####9 | 98/200 [00:04<00:05, 19.81it/s]
50%|##### | 100/200 [00:05<00:05, 19.80it/s]
51%|#####1 | 102/200 [00:05<00:04, 19.80it/s]
52%|#####2 | 104/200 [00:05<00:04, 19.80it/s]
53%|#####3 | 106/200 [00:05<00:04, 19.82it/s]
54%|#####4 | 108/200 [00:05<00:04, 19.82it/s]
55%|#####5 | 110/200 [00:05<00:04, 19.82it/s]
56%|#####6 | 112/200 [00:05<00:04, 19.82it/s]
57%|#####6 | 114/200 [00:05<00:04, 19.82it/s]
58%|#####8 | 116/200 [00:05<00:04, 19.84it/s]
59%|#####8 | 118/200 [00:05<00:04, 19.86it/s]
60%|###### | 120/200 [00:06<00:04, 19.85it/s]
61%|######1 | 122/200 [00:06<00:03, 19.86it/s]
62%|######2 | 124/200 [00:06<00:03, 19.84it/s]
63%|######3 | 126/200 [00:06<00:03, 19.85it/s]
64%|######4 | 128/200 [00:06<00:03, 19.84it/s]
65%|######5 | 130/200 [00:06<00:03, 19.84it/s]
66%|######6 | 132/200 [00:06<00:03, 19.84it/s]
67%|######7 | 134/200 [00:06<00:03, 19.83it/s]
68%|######8 | 136/200 [00:06<00:03, 19.82it/s]
69%|######9 | 138/200 [00:06<00:03, 19.83it/s]
70%|####### | 140/200 [00:07<00:03, 19.84it/s]
71%|#######1 | 142/200 [00:07<00:02, 19.84it/s]
72%|#######2 | 144/200 [00:07<00:02, 19.82it/s]
73%|#######3 | 146/200 [00:07<00:02, 19.81it/s]
74%|#######4 | 148/200 [00:07<00:02, 19.82it/s]
75%|#######5 | 150/200 [00:07<00:02, 19.83it/s]
76%|#######6 | 152/200 [00:07<00:02, 19.82it/s]
77%|#######7 | 154/200 [00:07<00:02, 19.83it/s]
78%|#######8 | 156/200 [00:07<00:02, 19.85it/s]
79%|#######9 | 158/200 [00:07<00:02, 19.85it/s]
80%|######## | 160/200 [00:08<00:02, 19.85it/s]
81%|########1 | 162/200 [00:08<00:01, 19.83it/s]
82%|########2 | 164/200 [00:08<00:01, 19.82it/s]
83%|########2 | 166/200 [00:08<00:01, 19.79it/s]
84%|########4 | 168/200 [00:08<00:01, 19.80it/s]
85%|########5 | 170/200 [00:08<00:01, 19.81it/s]
86%|########6 | 172/200 [00:08<00:01, 19.83it/s]
87%|########7 | 174/200 [00:08<00:01, 19.83it/s]
88%|########8 | 176/200 [00:08<00:01, 19.83it/s]
89%|########9 | 178/200 [00:08<00:01, 19.82it/s]
90%|######### | 180/200 [00:09<00:01, 19.82it/s]
91%|#########1| 182/200 [00:09<00:00, 19.81it/s]
92%|#########2| 184/200 [00:09<00:00, 19.81it/s]
93%|#########3| 186/200 [00:09<00:00, 19.81it/s]
94%|#########3| 188/200 [00:09<00:00, 19.81it/s]
95%|#########5| 190/200 [00:09<00:00, 19.81it/s]
96%|#########6| 192/200 [00:09<00:00, 19.82it/s]
97%|#########7| 194/200 [00:09<00:00, 19.81it/s]
98%|#########8| 196/200 [00:09<00:00, 19.81it/s]
99%|#########9| 198/200 [00:09<00:00, 19.81it/s]
100%|##########| 200/200 [00:10<00:00, 19.82it/s]
100%|##########| 200/200 [00:10<00:00, 19.82it/s]
[34182.934, 43421.61, 47456.305, 45641.91, 45211.62, 45208.023, 49329.67, 47089.375, 48799.06, 45048.363, 45992.934, 44793.47, 47413.43, 42621.984, 45774.5, 48832.21, 44147.6, 44925.855, 44013.57, 42650.727, 40381.22, 45737.98, 43222.41, 47194.24, 47653.9, 48577.816, 45462.85, 46155.29, 44872.887, 46700.285, 44147.95, 49916.4, 42315.65, 44532.695, 50489.215, 41475.527, 48864.766, 45461.664, 46162.9, 42052.523, 46956.863, 48356.727, 44851.02, 42894.95, 47696.38, 46564.395, 46742.57, 48065.176, 45180.95, 44933.07, 44647.97, 46552.44, 44284.785, 44997.29, 42109.664, 46499.363, 44503.695, 40617.94, 42564.09, 47237.23, 51798.445, 51024.37, 46146.184, 43109.363, 46003.934, 45597.637, 49902.156, 41796.492, 45516.504, 43430.727, 42417.645, 41554.895, 47655.227, 45988.79, 47447.215, 44695.67, 44216.63, 48585.434, 46739.36, 48723.004, 41341.32, 44293.54, 49171.297, 52826.426, 40180.64, 50103.26, 44449.805, 44869.355, 44629.945, 48514.17, 42393.24, 38409.46, 48071.72, 44697.15, 46758.37, 51898.47, 42264.18, 43256.93, 47687.8, 49400.227, 42400.91, 47261.613, 41499.28, 48537.2, 42841.203, 45859.145, 47135.69, 41100.516, 44988.754, 47567.36, 42426.96, 42813.875, 44998.34, 45227.047, 45983.945, 41886.016, 45702.047, 45630.465, 49407.594, 43054.39, 44540.0, 50300.137, 41913.94, 47806.89, 43730.23, 46277.266, 46316.65, 47477.914, 44759.61, 46698.953, 50030.684, 43481.44, 45230.91, 46141.855, 43181.04, 44675.316, 47656.176, 44109.355, 46311.047, 45429.01, 44876.996, 45847.184, 44171.285, 45450.45, 43761.496, 46614.734, 43720.246, 50092.99, 46857.926, 47100.57, 46701.875, 43790.39, 41562.35, 48829.16, 46667.32, 50557.594, 46151.53, 44773.87, 44658.105, 45546.92, 43993.727, 48417.785, 43276.816, 42826.16, 42172.28, 45177.79, 47810.8, 44513.91, 42780.8, 41627.293, 44821.047, 46628.55, 45888.64, 48440.234, 45328.7, 44922.25, 46871.13, 47178.785, 43550.82, 43593.4, 45235.98, 46922.234, 44772.91, 45723.85, 47051.785, 43760.2, 42936.15, 44696.88, 43665.773, 49126.69, 46679.52, 48033.504, 44735.92, 38833.477, 47059.895, 43743.934, 43696.63, 44852.36, 45082.41, 46031.746]
<AxesSubplot:title={'center':'Train loss against iterations'}>
Total running time of the script: ( 0 minutes 39.116 seconds)