Measuring CPU performance with a parallelized vector sum and AVX

The example compares the time spend in computing the sum of all coefficients of a matrix when the function walks through the coefficients by rows or by columns when the computation is parallelized or uses AVX instructions.

Vector Sum

from tqdm import tqdm
import numpy
import matplotlib.pyplot as plt
from pandas import DataFrame
from onnx_extended.ext_test_case import measure_time, unit_test_going
from onnx_extended.validation.cpu._validation import (
    vector_sum_array as vector_sum,
    vector_sum_array_parallel as vector_sum_parallel,
    vector_sum_array_avx as vector_sum_avx,
    vector_sum_array_avx_parallel as vector_sum_avx_parallel,
)

obs = []
dims = [500, 700, 800, 900, 1000, 1100, 1200, 1300, 1400, 1500, 1600, 1700, 1800, 2000]
if unit_test_going():
    dims = dims[:3]
for dim in tqdm(dims):
    values = numpy.ones((dim, dim), dtype=numpy.float32).ravel()
    diff = abs(vector_sum(dim, values, True) - dim**2)

    res = measure_time(lambda: vector_sum(dim, values, True), max_time=0.5)

    obs.append(
        dict(
            dim=dim,
            size=values.size,
            time=res["average"],
            direction="rows",
            time_per_element=res["average"] / dim**2,
            diff=diff,
        )
    )

    res = measure_time(lambda: vector_sum_parallel(dim, values, True), max_time=0.5)

    obs.append(
        dict(
            dim=dim,
            size=values.size,
            time=res["average"],
            direction="rows//",
            time_per_element=res["average"] / dim**2,
            diff=diff,
        )
    )

    diff = abs(vector_sum_avx(dim, values) - dim**2)
    res = measure_time(lambda: vector_sum_avx(dim, values), max_time=0.5)

    obs.append(
        dict(
            dim=dim,
            size=values.size,
            time=res["average"],
            direction="avx",
            time_per_element=res["average"] / dim**2,
            diff=diff,
        )
    )

    diff = abs(vector_sum_avx_parallel(dim, values) - dim**2)
    res = measure_time(lambda: vector_sum_avx_parallel(dim, values), max_time=0.5)

    obs.append(
        dict(
            dim=dim,
            size=values.size,
            time=res["average"],
            direction="avx//",
            time_per_element=res["average"] / dim**2,
            diff=diff,
        )
    )


df = DataFrame(obs)
piv = df.pivot(index="dim", columns="direction", values="time_per_element")
print(piv)

  0%|          | 0/14 [00:00<?, ?it/s]
  7%|7         | 1/14 [00:23<05:07, 23.69s/it]
 14%|#4        | 2/14 [00:29<02:38, 13.18s/it]
 21%|##1       | 3/14 [00:36<01:53, 10.31s/it]
 29%|##8       | 4/14 [00:39<01:15,  7.53s/it]
 36%|###5      | 5/14 [00:44<01:00,  6.69s/it]
 43%|####2     | 6/14 [00:48<00:46,  5.78s/it]
 50%|#####     | 7/14 [00:52<00:35,  5.01s/it]
 57%|#####7    | 8/14 [00:57<00:30,  5.03s/it]
 64%|######4   | 9/14 [01:02<00:25,  5.04s/it]
 71%|#######1  | 10/14 [01:07<00:20,  5.15s/it]
 79%|#######8  | 11/14 [01:11<00:13,  4.55s/it]
 86%|########5 | 12/14 [01:14<00:08,  4.30s/it]
 93%|#########2| 13/14 [01:17<00:03,  3.78s/it]
100%|##########| 14/14 [01:20<00:00,  3.64s/it]
100%|##########| 14/14 [01:20<00:00,  5.76s/it]
direction           avx         avx//          rows        rows//
dim
500        1.169482e-10  6.584677e-09  1.294117e-09  4.492941e-09
700        1.164437e-10  8.354547e-10  1.572818e-09  3.314939e-09
800        2.354458e-10  2.275965e-09  1.252802e-09  5.260128e-09
900        1.646671e-10  1.576197e-09  1.442125e-09  2.144507e-09
1000       2.336233e-10  1.399248e-09  1.777096e-09  3.377276e-09
1100       2.447942e-10  1.888272e-09  1.238211e-09  1.887679e-09
1200       2.531974e-10  6.634164e-10  1.330335e-09  2.130782e-09
1300       2.830117e-10  1.407723e-09  1.426193e-09  1.544761e-09
1400       2.648387e-10  1.611463e-09  1.474442e-09  1.899156e-09
1500       2.828198e-10  6.430161e-10  1.199285e-09  9.434222e-10
1600       2.950141e-10  1.053861e-09  1.338651e-09  1.315141e-09
1700       2.817763e-10  9.724717e-10  1.217194e-09  1.163081e-09
1800       2.738288e-10  7.743195e-10  1.427345e-09  9.821519e-10
2000       3.530068e-10  9.458257e-10  1.412058e-09  1.037141e-09

Plots

piv_diff = df.pivot(index="dim", columns="direction", values="diff")
piv_time = df.pivot(index="dim", columns="direction", values="time")

fig, ax = plt.subplots(1, 3, figsize=(12, 6))
piv.plot(ax=ax[0], logx=True, title="Comparison between two summation")
piv_diff.plot(ax=ax[1], logx=True, logy=True, title="Summation errors")
piv_time.plot(ax=ax[2], logx=True, logy=True, title="Total time")
fig.savefig("plot_bench_cpu_vector_sum_avx_parallel.png")

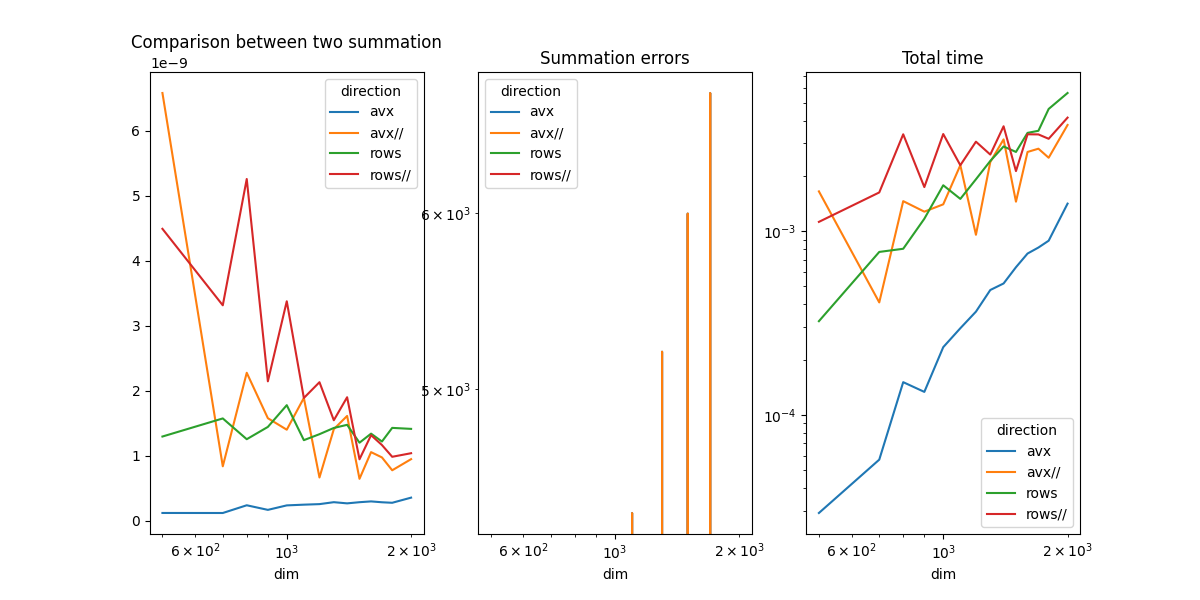
AVX is faster.